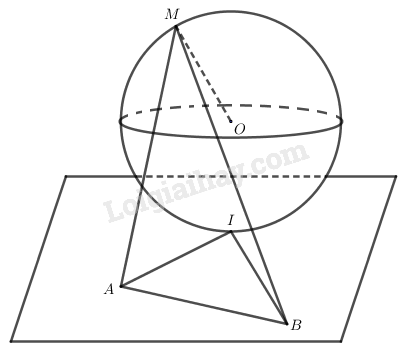
Đề bài
Gọi mặt cầu S(O;r) tiếp xúc với (P) tại I. Gọi M là một điểm nằm trên mặt cầu nhưng không phải là điểm đối xứng với I qua tâm O. Từ M kẻ hai tiếp tuyến cắt của mặt cầu cắt (P) tại A và B. Chứng minh rằng ^AMB=^AIB.
Phương pháp giải - Xem chi tiết
+) Áp dụng tính chất của hai tiếp tuyến cắt nhau.
+) Chứng minh hai tam giác bằng nhau suy ra các góc tương ứng bằng nhau.
Lời giải chi tiết
Do mặt cầu S(O; r) tiếp xúc với mp (P) tại I nên: OI ⊥ (P) ⇒ OI ⊥ IA
Suy ra, AI là tiếp tuyến của mặt cầu đã cho tại điểm I.
Theo tính chất của mặt cầu, ta có AI và AM là hai tiếp tuyến với cầu kẻ từ A, cho nên AI=AM, tương tự BI=BM
Hai tam giác ABI và ABM bằng nhau (c.c.c)
⇒^AMB=^AIB (Hai góc tương ứng).