Video hướng dẫn giải
Cho hàm số: \(\displaystyle y = - {1 \over 3}{x^3} + (a - 1){x^2} + (a + 3)x - 4.\)
LG a
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (C) của hàm số khi \(a = 0.\)
Phương pháp giải:
Thay \(a=0\) vào hàm số sau đó khảo sát và vẽ đồ thị hàm số theo các bước đã được học.
Lời giải chi tiết:
Khi \(a = 0\) ta có hàm số: \(\displaystyle y = - {1 \over 3}{x^3} - {x^2} + 3x - 4\)
- Tập xác định : \((-∞; +∞)\)
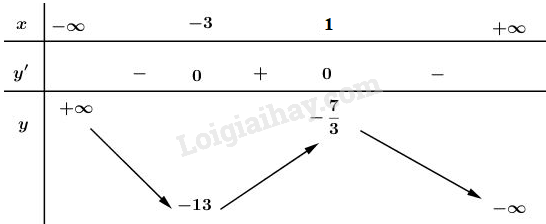
- Sự biến thiên: \(y’= -x^2 – 2x + 3\)
\(y’=0 ⇔ x = 1, x = -3\)
Trên các khoảng \((-∞;-3)\) và \((1; +∞), y’ < 0\) nên hàm số nghịch biến.
Trên khoảng \((-3; 1), y’ > 0\)
- Cực trị:
Hàm số đạt cực đại tại \(x = 1\), \(\displaystyle {y_{CD}} = {{ - 7} \over 3}\)
Hàm số đạt cực tiểu tại \(x = -3\), \({y_{CT}} = - 13\)
- Giới hạn vô cực: \(\mathop {\lim }\limits_{x \to + \infty } = - \infty ,\mathop {\lim }\limits_{x \to - \infty } = + \infty \)
Bảng biến thiên:
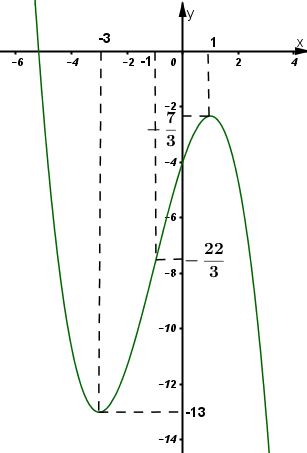
Đồ thị hàm số:
Đồ thị cắt trục tung tại \(y = -4\)
Đồ thị cắt trục hoành tại \(x ≈ 5, 18\)
LG b
b) Tính diện tích hình phẳng giới hạn bởi (C) và đường thẳng \(y = 0,\, x = -1,\, x = 1.\)
Phương pháp giải:
Hình phẳng được giới hạn bởi đường các đồ thị hàm số \(y=f(x);\) \(y=g(x)\) và các đường thẳng \(x=a; \, \, x=b \, (a<b)\) có diện tích được tính bởi công thức: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx.} \)
Lời giải chi tiết:
Hàm số \(y = - {1 \over 3}{x^3} - {x^2} + 3x - 4\) đồng biến trên khoảng \((-3; 1)\) nên:
\(y < y(1) = {{ - 7} \over 3} < 0\), \(∀x ∈ (-1; 1)\)
Do đó , diện tích cần tính là:
\(\begin{array}{l}
S = \int\limits_{ - 1}^1 {\left| { - \dfrac{1}{3}{x^3} - {x^2} + 3x - 4} \right|dx} \\ = \int\limits_{ - 1}^1 {\left( {\dfrac{1}{3}{x^3} + {x^2} - 3x + 4} \right)dx} \\
\;\; = \left. {\left( {\dfrac{{{x^4}}}{{12}} + \dfrac{{{x^3}}}{3} - \dfrac{{3{x^2}}}{2} + 4x - 1} \right)} \right|_{ - 1}^1 \\ = \dfrac{{23}}{{12}} + \dfrac{{27}}{4} = \dfrac{{26}}{3}.
\end{array}\)