Đề bài
Câu 1. Điểm cực đại của hàm số y=x4−8x2+1 là
A. x=2 B. x=−2
C. x=±2 D. x=0.
Câu 2. Tìm điểm cực tiểu của đồ thị hàm số y=−13x3+x
A. (−1;0)
B. (1;23)
C. (−1;−23)
D. (1;0)
Câu 3. Nếu hàm số y=f(x) thỏa mãn lim thì đồ thị hàm số y=f(x) có đường tiệm cận đứng là đường có phương trình
A. x = 1 B. y = 1
C. x = - 1 D. y = - 1.
Câu 4. Hàm số nào sau đây mà đồ thị không có đường tiệm cận ?
A. y = \dfrac{{ - 2x + 5}}{{x - 3}}
B. y = 2{x^3} - x + 2
C. y = \dfrac{{x - 2}}{{x + 3}}
D. y = \dfrac{{3x - 2}}{{x + 1}}
Câu 5. Trong các mệnh đề sau mệnh đề nào sai:
A. Nếu f'(x) > 0,\forall x \in K thì hàm số f(x) đồng biến trên K.
B. Nếu f'(x) \ge 0,\forall x \in K và dấu “=” xảy ra tại hữu hạn điểm thì hàm số f(x) đồng biến trên K.
C. Hàm số y=f(x) là hàm hằng trên K khi f'(x) = 0,\forall x \in K
D. Nếu f'(x) > 0,\forall x \in K thì hàm số f(x) nghịch biến trên K.
Câu 6. Viết phương trình tiếp tuyến của đồ thị hàm số y = \dfrac{{2x}}{{x - 2}} tại điểm có hoành độ bằng 3:
A. y = 4x - 18
B. y = - 4x + 18
C. y = - 4x + 6
D. y = - 4x - 18
Câu 7. Đồ thị sau đây là của hàm số nào ?
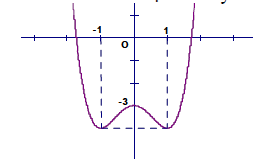
A. y = - {x^4} + 2{x^2} - 3
B. y = {x^4} + 3{x^2} - 3
C. y = {x^4} - 2{x^2} - 3
D. y = {x^4} - 2{x^2} + 3
Câu 8. Cho hàm số y = {x^3} + 3x + 2. Mệnh đề nào dưới đây là đúng ?
A. Hàm số nghịch biến trên khoảng ( - \infty ;0) và đồng biến trên khoảng (0; + \infty ).
B. Hàm số đồng biến trên khoảng ( - \infty ; + \infty ).
C. Hàm số đồng biến trên khoảng ( - \infty ;0) và nghịch biến trên khoảng (0; + \infty ).
D. Hàm số nghịch biến trên khoảng ( - \infty ; + \infty ).
Câu 9. Hàm số y = {x^4} - 8{x^3} + 432 có bao nhiêu điểm cực trị?
A. 0 B. 1
C. 2 D. 3 .
Câu 10. Hàm số y = {x^4} - 2{x^2} + 2016 nghịch biến trên khoảng nào sau đây?
A. (- 1 ; 0) B . ( - \infty ; - 1)
C. (- 1 ;1) D. ( - \infty ;1)
Lời giải chi tiết
| Câu | 1 | 2 | 3 | 4 | 5 |
| Đáp án | D | C | A | B | D |
| Câu | 6 | 7 | 8 | 9 | 10 |
| Đáp án | B | C | B | B | B |
Câu 1. Ta có y' = 4{x^3} - 16x,\,\,y' = 0
\Leftrightarrow 4{x^3} - 16x = 0
\Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\\x = - 2\end{array} \right.
Ta có bảng biến thiên:
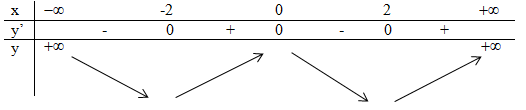
Đồ thị hàm số đạt cực đại tại x= 0.
Chọn D.
Câu 2. y' = - {x^2} + 1,\,\,y' = 0
\Rightarrow \,\, - {x^2} + 1 = 0\,\, \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.
Ta có bảng biến thiên:
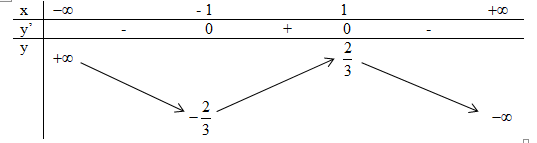
Đồ thị hàm số đạt cực tiểu tại x = - 1,
y(- 1)= - \dfrac{2}{3}.
Vậy điểm cực tiểu là \left( { - 1; - \dfrac{2}{3}} \right) .
Chọn C.
Câu 3:
\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = - \infty nên đồ thị hàm số nhận x = 1 làm TCĐ.
Chọn A.
Câu 4:
Đồ thị hàm số bậc ba không có đường tiệm cận.
Chọn B.
Câu 5:
Nếu f'\left( x \right) > 0 với mọi x \in K thì hàm số y = f\left( x \right) đồng biến trên K.
Vậy D sai.
Chọn D.
Câu 6. Ta có y' = \dfrac{{ - 4}}{{{{\left( {x - 2} \right)}^2}}},
y'(3) = - 4,\,\,y(3) = 6
Vậy phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 3 là
y = - 4 (x-3) + 6
\Rightarrow y= - 4x +18
Chọn B.
Câu 7. Đồ thị hàm số có a > 0 nên loại A, điểm (1 ; - 4) thuộc đồ thị hàm số nên câu C thỏa mãn.
Chọn C.
Câu 8. y' = 3{x^2} + 3 > 0,\forall x \in R .
Vậy hàm số đồng biến trên \left( { - \infty ; + \infty } \right)
Chọn B.
Câu 9. y' = 4{x^3} - 24{x^2},\,\,y' = 0
\Rightarrow \,\,\,4{x^3} - 24{x^2} = 0
\Leftrightarrow \,\,\left[ \begin{array}{l}x = 0\\x = 6\end{array} \right.
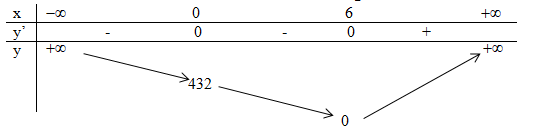
Vậy đồ thị hàm số trên có 1 điểm cực trị vì x = 0 là nghiệm kép của phương trình y’ = 0.
Chọn B.
Câu 10. Ta có y' = 4{x^3} - 4x,\,\,y' = 0
\Rightarrow \,4{x^3} - 4x = 0
\Leftrightarrow \,\,\left[ \begin{array}{l}x = 0\\x = - 1\\x = 1\end{array} \right.
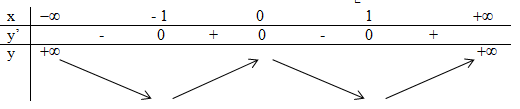
Vậy hàm số nghịch biến trên các khoảng
Chọn B.

