Đề bài
Cho hình chóp \(S.ABC\) có bốn đỉnh đều nằm trên một mặt cầu, \(SA = a, SB = b, SC = c\) và ba cạnh \(SA, SB, SC\) đôi một vuông góc. Tính diện tích mặt cầu và thể tích khối cầu được tạo bởi mặt cầu đó.
Phương pháp giải - Xem chi tiết
+) Công thức tính diện tích mặt cầu bán kính \(r\) là: \(S=4 \pi r^2.\)
+) Công thức tính thể tích mặt cầu bán kính \(r\) là: \(V=\dfrac{4}{3} \pi r^3.\)
Lời giải chi tiết
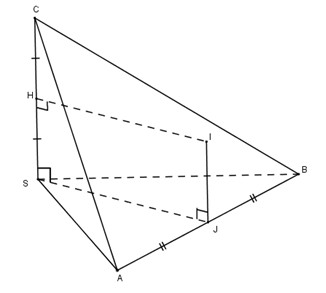
Gọi \(I\) là tâm mặt cầu ngoại tiếp hình chóp tam giác \(S.ABC\). Hạ \(IJ\) vuông góc \((SAB)\), vì \(I\) cách đều \(3\) điểm \(S, A, B\) nên \(J\) cũng cách đều \(3\) điểm \(S, A, B\).
Vì tam giác \(SAB\) vuông đỉnh \(S\) nên \(J\) là trung điểm của \(AB\).
Ta có \(SJ ={1 \over 2}AB = {1 \over 2}\sqrt {{a^2} + {b^2}}\)
Do \(SC\) vuông góc \((SAB)\) nên \(IJ // SC\).
Gọi \(H\) là trung điểm \(SC\), ta có \(SC=SI\) nên \(IH \bot SC \).
Xét tứ giác \(SHIJ\) ta có: \( \widehat {SHI}= 90 ^0\) do \(IH \bot SC \);
\( \widehat {HSJ}= 90 ^0\) do \(SC \bot (SAB) \) chứa \(SJ\);
\(\widehat {IJS}\) do \(IJ \bot (SAB) \) chứa \(SJ\)
Suy ra tứ giác \(SHIJ\) là hình chữ nhật.
\(\rightarrow SH = IJ = {c \over 2}\).
Do vậy, \(I{S^2} = I{J^2} + S{J^2} = {{({a^2} + {b^2} + {c^2})} \over 4}\) và bán kính hình cầu ngoại tiếp \(S.ABC\) là
\(R = IS = {1 \over 2}\sqrt {{a^2} + {b^2} + {c^2}} \)
Diện tích mặt cầu là:
\(S = 4\pi {R^2} = \pi ({a^2} + {b^2} + {c^2})\)
\( \Rightarrow \Delta //SC\)
Do đó mọi điểm trên \(\Delta\) cách đều S,A,B. (Theo bài 3)
Dựng mặt phẳng trung trực của SC cắt \(Delta\) tại I.
Khi đó ta có: \(IS=IC\).
\(I \in \Delta \Rightarrow IA=IS=IB\). Vậy I là tâm đường tròn ngoại tiếp S.ABC

