Phần 1
ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Câu 1. Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
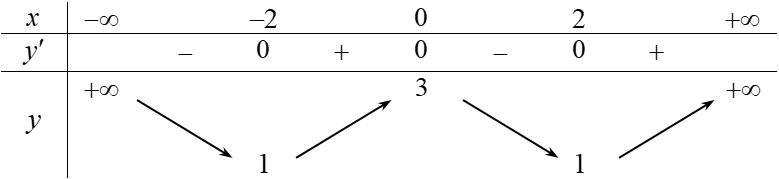
Hàm số đã cho nghịch biến trên khoảng nào dưới đây.
A. \(\left( {0; + \infty } \right)\). B. \(\left( {0;3} \right)\).
C. \(\left( { - 2;0} \right)\). D. \(\left( { - \infty ; - 2} \right)\).
Câu 2. Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
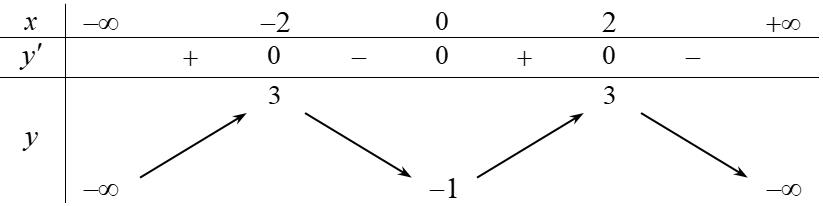
Hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng nào dưới đây?
A. \(\left( { - 2;2} \right)\). B. \(\left( { - \infty ;\, - 2} \right)\).
C. \(\left( {0;\,2} \right)\). D. \(\left( {3; + \infty } \right)\).
Câu 3. Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên dưới.
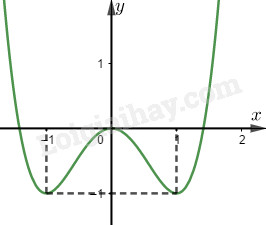
Khẳng định nào sau đây sai?
A. Hàm số đồng biến trên khoảng \(\left( { - 1;0} \right)\).
B. Hàm số nghịch biến trên khoảng \(\left( { - 1;3} \right)\).
C. Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\).
D. Hàm số nghịch biến trên khoảng \(\left( {0;\dfrac{1}{2}} \right)\).
Câu 4. Hàm số \(y = - {x^3} + 3{x^2} + 3\) đồng biến trên khoảng
A. \(\left( { - \infty ;1} \right)\). B. \(\left( {0;2} \right)\).
C. \(\left( {2; + \infty } \right)\). D. \(\mathbb{R}\).
Câu 5. Hàm số \(y = {x^4} - 2{x^2} + 1\) nghịch biến trên
A. \(\left( { - \infty ; - 1} \right)\,\)và \(\left( {0,1} \right)\). B. \(\left( { - 1,0} \right)\) và \(\left( {1, + \infty } \right)\).
C. \(\mathbb{R}\). D. \(\left( { - \sqrt 2 ,\sqrt 2 } \right)\).
Câu 6. Hàm số \(y = \dfrac{{x - 1}}{{x - 3}}\) nghịch biến trên
A. \(\mathbb{R}\). B. \(\left( { - \infty ;3} \right)\).
C. \(\left( { - 3; + \infty } \right)\). D.\(\left( { - \infty ;3} \right){\rm{;}}\left( { - 3; + \infty } \right)\).
Câu 7. Hàm số nào sau đây đồng biến trên khoảng \(\left( { - \infty ; - 1} \right)\).
A. \(y = 2{x^3} - 3{x^2} - 12x + 4\).
B. \(y = 2{x^3} + 3{x^2} - 12x + 4\).
C. \(y = - 2{x^3} - 3{x^2} + 12x - 4\).
D. \(y = - 2{x^3} + 3{x^2} + 12x - 4\,\).
Câu 8. Cho hàm số \(f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) là \(f'\left( x \right) = {\left( {x + 1} \right)^4}\left( {x - 1} \right)\). Hàm số đã cho đồng biến trên khoảng
A. \(\left( {1; + \infty } \right)\). B. \(\left( { - \infty ; + \infty } \right)\).
C. \(\left( { - 1;1} \right)\). D. \(\left( { - \infty ;1} \right)\).
Câu 9. Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = \left( {x + 2} \right){\left( {x - 1} \right)^{2021}}{\left( {x - 2} \right)^{2020}}\). Khẳng định nào sau đây đúng?
A. Hàm số đạt cực đại tại điểm \(x = 1\) và đạt cực tiểu tại các điểm \(x = \pm 2\).
B. Hàm số đồng biến trên mỗi khoảng \(\left( {1\,;\,2} \right)\) và \(\left( {2\,;\, + \infty } \right)\).
C. Hàm số có ba điểm cực trị.
D. Hàm số đồng biến trên khoảng \(\left( { - 2\,;\,1} \right)\).
Câu 10. Cho hàm số \(y = f\left( x \right)\).Hàm số \(y = f'\left( x \right)\)có đồ thị như hình bên. Hàm số \(y = f\left( {2 - x} \right)\) đồng biến trên khoảng:
A. \(\left( {1;3} \right)\). B. \(\left( {2; + \infty } \right)\).
C. \(\left( { - 2;1} \right)\). D. \(\left( { - \infty ;2} \right)\).
Câu 11. Cho hàm số \(f\left( x \right)\) xác định trên tập số thực \(\mathbb{R}\) và có đồ thị \(f'\left( x \right)\)như hình sau. Đặt \(g\left( x \right) = f\left( x \right) - x\), hàm số \(g\left( x \right)\) nghịch biến trên khoảng:
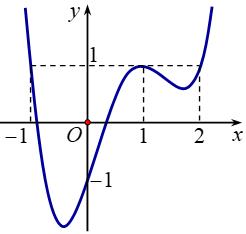
A. \(\left( {1; + \infty } \right)\). B. \(\left( { - 1;\,2} \right)\).
C. \(\left( {2;\, + \infty } \right)\). D. \(\left( { - \infty ; - 1} \right)\).
Câu 12. Tìm \(m\) để hàm số \(y = {x^2}\left( {m - x} \right) - 2018\) \(\left( 1 \right)\)đồng biến trên khoảng \(\left( {1 ;2} \right)\).
A. \(m \in {\rm{[3; + }}\infty )\). B. \(m \in {\rm{[}}0; + \infty )\).
C. \(m \in {\rm{[}} - 3; + \infty )\). D. \(m \in ( - \infty ; - 1]\).
Câu 13. Có bao nhiêu giá trị nguyên \(m\) để hàm số \(y = \frac{{x + 2}}{{x - m}}\) nghịch biến trên khoảng \(\left( {5; + \infty } \right)\)
A. 7. B. 8. C. 9. D. 10.
Câu 14. Tìm giá trị lớn nhất \(M\)của hàm số \(y = \frac{{3x - 1}}{{x - 3}}\) trên đoạn \(\left[ {0\,;\,2} \right]\).
A. \(M = 5\). B. \(M = - 5\).
C. \(M = \dfrac{1}{3}\). D. \(M = - \dfrac{1}{3}\).
Câu 15. Tìm tất cả các giá trị thực của \(m\) để bất phương trình \(2{x^4} - 4{x^2} - 10 \ge m\) nghiệm đúng với mọi\(x \in \left( - \infty ; - 1 \right]\)?
A. \(m \le - 12\). B. \(m \le 12\).
C. \(m \le - 8\). D. \(m \in \emptyset \).
Câu 16. Cho đồ thị một hàm số có hình vẽ như hình dưới đây.
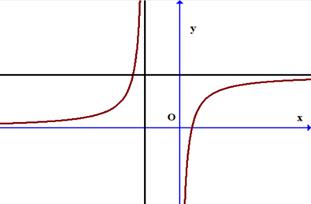
Hỏi đồ thị trên có bao nhiêu đường tiệm cận?
A. \(4\). B. Không có tiệm cận.
C. \(2\). D. 3.
Câu 17. Tìm tất cả các giá trị thực của tham số \(m\) sao cho đồ thị hàm số \(y = \frac{{{x^2} - mx - 2{m^2}}}{{x - 2}}\) có đường tiệm cận đứng.
A. \(\left[ \begin{array}{l}m \ne - 2\\m \ne 1\end{array} \right.\). B. Không có \(m\) thỏa mãn.
C. \(\left\{ \begin{array}{l}m \ne - 2\\m \ne 1\end{array} \right.\). D. \(m \in \mathbb{R}\).
Câu 18. Đồ thị hình bên là đồ thị của hàm số nào trong các hàm số sau
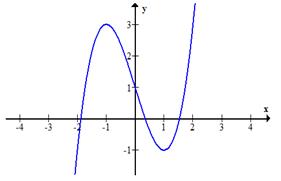
A. \(y = - {x^3} + 3{x^2} + 1\). B. \(y = {x^3} - 3x - 1\).
C. \(y = {x^3} - 3x + 1\). D. \(y = - {x^3} - 3{x^2} - 1\).
Câu 19. Đồ thị sau đây là của hàm số nào?
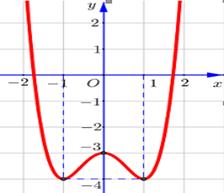
A. \(y = {x^4} + 2{x^2} - 3\). B. \(y = {x^4} - 3{x^2} - 3\).
C. \(y = {x^4} - 2{x^2} - 3\). D. \(y = - \dfrac{1}{4}{x^4} + 3{x^2} - 3\).
Câu 20. Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Phương trình \(f\left( x \right) - 3 = 0\) có mấy nghiệm?
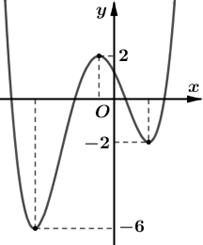
A. \(2\). B. \(3\). C. \(1\). D. \(4\).
Câu 21. Cho hàm số \(y = {x^4} - 2{x^2} + 1\) có đồ thị \(\left( C \right)\) và đường thẳng \(\left( d \right):\,y = m + 1\) (\(m\) là tham số). Đường thẳng \(\left( d \right)\) cắt \(\left( C \right)\) tại \(4\) điểm phân biệt khi các giá trị của \(m\) là
A. \(3 < m < 5\). B. \(1 < m < 2\).
C. \( - 1 < m < 0\). D. \( - 5 < m < - 3\).
Câu 22. Hàm số nào sau đây có bảng biến thiên như hình bên:
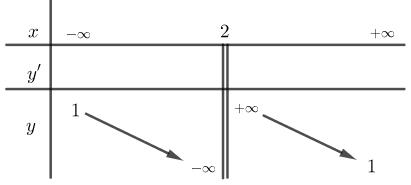
A. \(y = \dfrac{{2x - 5}}{{x - 2}}\). B. \(y = \dfrac{{x + 3}}{{x - 2}}\).
C. \(y = \dfrac{{2x + 2}}{{x - 2}}\). D. \(y = \dfrac{{x - 4}}{{x - 2}}\).
Câu 23. Có bao nhiêu giá trị nguyên không âm m để hàm số \(y = \left| {{x^4} - m{x^2} + 9} \right|\) đồng biến trên khoảng \(\left( {1; + \infty } \right)\)
A. 3 B. 6. C. 7 D. 4
Phần 2
HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
Câu 1. Tính đạo hàm của hàm số \(y = \ln \left( {x - {x^2}} \right)\)
A. \(y' = 1 - 2x\) B. \(y' = \dfrac{{1 - 2x}}{{x - {x^2}}}\)
C. \(y' = \dfrac{1}{{x - {x^2}}}\) D. \(y' = x - {x^2}\)
Câu 2. Tính đạo hàm của hàm số \(y = \dfrac{1}{{{{10}^x}}}\)
A. \(y' = - \dfrac{1}{{{{10}^x}}}\) B. \(y' = - \dfrac{{\ln 10}}{{{{10}^x}}}\)
C. \(y' = \dfrac{{\ln 10}}{{{{10}^x}}}\) D. \(y' = \dfrac{1}{{{{10}^x}}}\)
Câu 3. Cho \({\bf{a}},{\bf{b}}\) dương và \(a \ne 1\). Khẳng định nào sau đây đúng?
A. \({\log _{{a^3}}}\left( {ab} \right) = 3 + 3{\log _a}b\)
B. \({\log _{{a^3}}}\left( {ab} \right) = \dfrac{1}{3}{\log _a}b\)
C. \({\log _{{a^3}}}\left( {ab} \right) = \dfrac{1}{3} + \dfrac{1}{3}{\log _a}b\)
D. \({\log _{{a^3}}}\left( {ab} \right) = 3{\log _a}b\)
Câu 4. Nghiệm của phương trình \({\left( {\sqrt 2 - 1} \right)^x} = {\left( {3 - 2\sqrt 2 } \right)^{x + 2}}\) là
A. \(x = 0\)
B. \(x = - 4\)
C. \(x = - 2\)
D. \(x = - 2;x = - 4\)
Câu 5. Giải phương trình \({\log _3}\left( {x - 1} \right) = {\log _3}\left( {{x^2} - x} \right) - 2\)
A. \(x = 9\)
B. \(x = 1\)
C. \(x = 1;x = 9\)
D. \(x = 3\)
Câu 6. Bất phương trình \({3^{{x^2} + 2x}} \le 27\) có nghiệm là:
A. \( - 3 \le x \le 1\)
B. \(\left[ \begin{array}{l}x \ge 1\\x \le - 3\end{array} \right.\)
C. \( - 1 \le x \le 3\)
D. \(\left[ \begin{array}{l}x \ge 3\\x \le - 1\end{array} \right.\)
Câu 7. Một người gửi tiết kiệm 100 triệu đồng với lãi suất kép theo quý là \(2\% \). Hỏi sau 2 năm người đó lấy lại cả gốc lẫn lãi là bao nhiêu tiền?
A. \(17,1\) triệu
B. \(16\) triệu
C. \(117,1\)triệu
D. \(116\) triệu
Câu 8. Cường độ một trận động đất được đo bởi công thức \(M = \log A - \log {A_0}\) với A là biên độ rung chấn tối đa, \({A_0}\) là biên độ chuẩn (hằng số). Đầu thế kỉ 20, một trận động đất ở San Francisco có cường độ đo được 8 độ Richter. Trong cùng năm đó trận động đất khác ở Nhật Bản có cường độ đo được 6 độ Richter. Hỏi trận động đất ở San Francisco có biên độ gấp bao nhiêu lần biên độ trận động đất ở Nhận Bản?
A. 1000 lần B. 10 lần C. 2 lần D. 100 lần
Câu 9. Giả sử \({x_1},{x_2}\) là hai nghiệm của phương trình \({\log _3}\left( {{3^x} - 1} \right).{\log _3}\left( {{3^{x + 1}} - 3} \right) = 6\). Khi đó \(\left( {{3^{{x_1}}} - 1} \right)\left( {{3^{{x_2}}} - 1} \right)\) có giá trị bằng?
A. \( - 6\) B. \(\dfrac{{280}}{{27}}\) C. \(\dfrac{1}{3}\) D. 3
Câu 10. Cho phương tình \({4^x} + {2^{x + 1}} - 3 = 0\). Số nghiệm của phương trình là
A. 0 B. 1 C. 2 D. 3
Phần 3
KHỐI ĐA DIỆN
Câu 1. Một hình chóp có \(4n\) cạnh \(\left( {n \in \mathbb{N},\,\,n \ge 1} \right)\) thì hình chóp này có bao nhiêu đỉnh?
A. \(4n\). B. \(n + 1\)
C. \(2n + 1\). D. \(2n\).
Câu 2. Một hình lăng trụ có số mặt bằng 12 thì hình này có bao nhiêu đỉnh?
A. 24. B. 10 C. 12. D.20.
Câu 3. Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng ?
A. \(3.\) B. \(2.\) C. \(4.\) D. \(6.\)
Câu 4. Hình đa diện trong hình vẽ có bao nhiêu mặt?
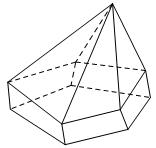
A. \(12\).
B. \(10\).
C. \(6\).
D. \(11\).
Câu 5. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, hình chiếu của điểm S trên mặt phẳng đáy thuộc miền trong của tam giác ABC, mặt bên (SAB) tạo với đáy góc \({45^0}\) và diện tích tam giác SAB bằng \(\dfrac{{{a^2}\sqrt 2 }}{4}.\)Tìm thể tích khối chóp trên.
A. \(\dfrac{{{a^3}}}{{12}}\). B. \(V = \dfrac{{{a^3}}}{{16}}\).
C. \(V = \dfrac{{{a^3}\sqrt 2 }}{{14}}\). D. \(\dfrac{{{a^3}\sqrt 3 }}{{24}}\).
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 3a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết góc giữa SC và ABCD bằng \(60^\circ \).
A. \({V_{S.ABC{\rm{D}}}} = 18{a^3}\sqrt 3 \)
B. \({V_{S.ABC{\rm{D}}}} = 9{a^3}\sqrt 3 \)
C. \({V_{S.ABC{\rm{D}}}} = 18{a^3}\sqrt {15} \)
D. \({V_{S.ABC{\rm{D}}}} = \dfrac{{9{a^3}\sqrt {15} }}{2}\)
Câu 7. Cho khối hộp chữ nhật \(ABCD.A'B'C'D'\) có thể tích bằng \(2110\). Biết \(A'M = MA\); \(DN = 3ND'\); \(CP = 2PC'\). Mặt phẳng \(\left( {MNP} \right)\) chia khối hộp đã cho thành hai khối đa diện. Thể tích khối đa diện nhỏ hơn bằng
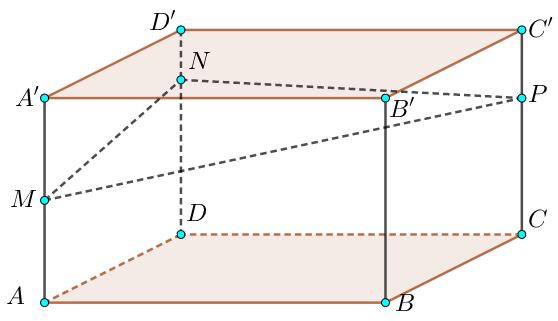
A. \(\dfrac{{7385}}{{18}}\). B. \(\dfrac{{5275}}{{12}}\).
C. \(\dfrac{{8440}}{9}\). D. \(\dfrac{{5275}}{6}\).
Câu 8. Cho hình hộp \(ABCD.A'B'C'D'\) có \(M\), \(N\) lần lượt trung điểm \(AA'\), \(CC'\). \({V_1}\) là thể tích khối đa diện chứa đỉnh \(A\) và \({V_2}\) là thể tích khối đa diện còn lại. Tính tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}.\)
A. \(2.\) B. \(\dfrac{1}{2}.\) C. \(1.\) D. \(\dfrac{2}{3}.\)
Câu 9. Cho hình chóp \(S.ABC\) có \(SA = a,\;SB = b,\;SC = c\) và \(\widehat {ASB} = \widehat {BSC} = \widehat {CSA} = 60^\circ \). Tính thể tích khối chóp \(S.ABC\) theo \(a,\;b,\;c.\)
A. \(\dfrac{{\sqrt 2 }}{{12abc}} \cdot \) B. \(\dfrac{{\sqrt 2 }}{{12}}abc.\)
C. \(\dfrac{{\sqrt 2 }}{4}abc.\) D. \(\dfrac{{\sqrt 2 }}{{4abc}} \cdot \)
Câu 10. Tính thể tích V của khối lăng trụ đều ABC.A’B’C’ biết \(AB = a,AB' = {\rm{ }}2a\)
A. \(V = \dfrac{{{a^3}\sqrt 3 }}{2}\) B. \(V = \dfrac{{{a^3}\sqrt 3 }}{4}\)
C. \(V = \dfrac{{3{a^3}}}{4}\) D. \(V = \dfrac{{{a^3}\sqrt 3 }}{{12}}\)
Phần 4
KHỐI TRÒN XOAY
Câu 1. Cho hình nó có chiều cao bằng \(2\sqrt 5 \). Một mặt phẳng đi qua đỉnh nón và cắt hình nón theo môt thiết diện là tam giác đều có diện tích bằng \(9\sqrt 3 \). Thể tích của hình nón được giới hạn bởi hình nón đã cho bằng
A. \(\dfrac{{32\sqrt 5 \pi }}{3}\) B. \(32\pi \)
C. \(32\sqrt 5 \pi \) D. \(96\pi \)
Câu 2. Cho tam giác ABC có AB=3, BC=5, AC=4. Thể tích của vật thể tròn xoay khi quay tam giác ABC quanh cạnh AC bằng
A. \(V = 12\pi \) B. \(V = 11\pi \)
C. \(V = 10\pi \) D. \(V = 13\pi \)
Câu 3. Hình nón (N) có đường sinh tạo với đáy một góc \(60^\circ \). Thiết diện qua trục của (N) là tam giác có bán kính đường tròn nội tiếp là 1. Thể tích của khối nón đã cho bằng
A. \(9\sqrt 3 \pi \) B. \(9\pi \)
C. \(3\sqrt 3 \pi \) D. \(3\pi \)
Câu 4. Tính thể tích V của khối trụ có bán kính đáy \({\rm{r}} = 4\) và chiều cao \(h = 5\).
A. \(V = 20\pi \) B. \(V = 40\pi \)
C. \(V = 100\pi \) D. \(V = 80\pi \)
Câu 5. Cho hình trụ có bán kính đáy bằng 9, thể tích bằng \(18\pi \). Diện tích xung quanh của hình trụ bằng
A. \(S = 18\pi \) B. \({\rm{S}} = 2\pi \)
C. \({\rm{S}} = 4\pi \) D. \({\rm{S}} = 8\pi \)
Câu 6. Cho khối trụ có thiết diện qua trục là một hình vuông có chu vi 8a. Thể tích của khối trụ đã cho bằng
A. \(3\pi {a^3}\) B. \(2{\pi ^2}{a^3}\)
C. \(\pi {a^3}\) D. \(2{\pi ^3}\)
Câu 7. Cắt một khối trụ cao 18cm bởi một mặt phẳng, ta được khối hình dưới đây. Biết rằng thiết diện là một elip, khoảng cách từ điểm thuộc thiết diện gần đáy nhất và điểm thuộc thiết diện xa mặt đáy nhất lần lượt là 8cm và 14cm. Tính tỉ số thể tích của hai khối được chia ra (khối nhỏ chia khối lớn).
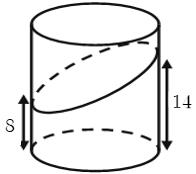
A. \(\dfrac{2}{{11}}\) B. \(0,5\) C. \(\dfrac{5}{{11}}\) D. \(\dfrac{7}{{11}}\)
Câu 8. Mặt phẳng \((P)\) cắt khối cầu tâm O theo đường tròn có bán kính bằng 4cm và khoảng cách từ O đến mặt phẳng \((P)\) bằng 3cm. Bán kính R của mặt cầu bằng
A. \(3\sqrt 3 \) cm
B. 5 cm
C. \(3\sqrt 2 \) cm
D. 6 cm
Câu 9. Mặt cầu (S) có diện tích bằng \(36\pi \). Bán kính và thể tích của khối cầu lần lượt là
A. \(36\) và 3
B. \(36\pi \) và 3
C. 3 và 36
D. 3 và \(36\pi \)
Câu 10. Cho hình chóp tam giác đều có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng \(45^\circ \). Mặt cầu ngoại tiếp hình chóp có bán kính bằng
A. \(\dfrac{{a\sqrt 3 }}{2}\) B. \(\dfrac{{a\sqrt 3 }}{3}\)
C. \(a\sqrt 3 \) D. \(\dfrac{{a\sqrt 3 }}{5}\)
Câu 11. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng \(3{\rm{a}}\sqrt 2 \), cạnh bên bằng 5a. Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD bằng
A. \(a\sqrt 3 \) B. \(a\sqrt 2 \)
C. \(\dfrac{{25{\rm{a}}}}{8}\) D. \(2{\rm{a}}\)
Câu 12. Cho hình lăng trụ tam giác đều có các cạnh đều bằng 2a. Diện tích mặt cầu ngoại tiếp hình lẳng trụ đó bằng
A. \(7\pi {a^2}\) B. \(\dfrac{{7\pi {{\rm{a}}^2}}}{3}\)
C. \(\dfrac{{7\pi {a^2}}}{2}\) D. \(\dfrac{{7\pi {{\rm{a}}^2}}}{6}\)

