Đề bài
Chứng minh rằng một đa diện mà mỗi đỉnh của nó đều là đỉnh chung của số lẻ mặt thì tổng số các đỉnh của nó là một số chẵn. Cho ví dụ.
Video hướng dẫn giải
Lời giải chi tiết
Giả sử đa diện \((H)\) có các đỉnh là \(A_1, … A_d\), gọi \(m_1, … m_d\) lần lượt là số các mặt của \((H)\) nhận chúng là đỉnh chung, ở đó \(m_1, … m_d\) là những số lẻ.
Như vậy mỗi đỉnh \(A_k\) có \(m_k\) cạnh đi qua.
Ta có: đỉnh \(A_1\) có \(m_1\) cạnh đi qua.
đỉnh \(A_2\) có \(m_2\) cạnh đi qua.
...
đỉnh \(A_d\) có \(m_d\) cạnh đi qua.
Do đó số các cạnh (có thể trùng nhau) của đa diện là \(m_1+m_2+...+m_d\).
Tuy nhiên, do mỗi cạnh là cạnh chung của đúng hai mặt nên số cạnh ở trên được đếm hai lần.
Vậy số cạnh thực tế của \((H)\) bằng
\(c = {\dfrac 1 2}({m_1} + {m_2} + ... + {m_d})\)
Vì \(c\) là số nguyên, \(m_1, … m_d\) là những số lẻ nên \(d\) phải là số chẵn.
Ví dụ : Hình chóp ngũ giác.
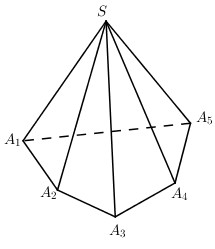
Đỉnh \(S\) là đỉnh chung của 5 mặt, tất cả các đỉnh còn lại là đỉnh chung của 3 mặt, hình chóp ngũ giác có 6 đỉnh.

