Video hướng dẫn giải
Bằng cách khảo sát hàm số, hãy tìm số nghiệm của các phương trình sau:
LG a
\({x^3}-3{x^2} + 5 = 0\);
Phương pháp giải:
+) Khảo sát sự biến thiên của các hàm số \(y=f\left( x \right)\) lập bảng biến thiên, vẽ đồ thị hàm số.
+) Số nghiệm của phương trình \(f\left( x \right)=a\) là số giao điểm của đồ thị hàm số \(y=f\left( x \right)\) với đường thẳng \(y=a.\)
+) Khi đó dựa vào đồ thị hàm số để xác định số giao điểm và kết luận.
Lời giải chi tiết:
Xét hàm số: \(y={{x}^{3}}-3{{x}^{2}}+5\)
+) Tập xác định: \(D=R.\)
+) Sự biến thiên:
Ta có: \(y'=3{{x}^{2}}-6x\Rightarrow y'=0\) \(\Leftrightarrow 3{{x}^{2}}-6x=0\) \(\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=2 \\ \end{align} \right..\)
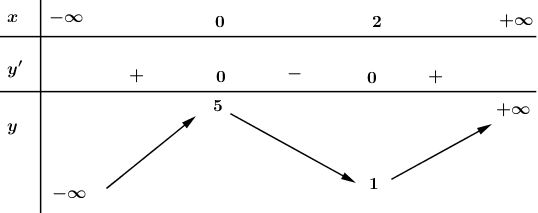
Hàm số đồng biến trên khoảng \(\left(- \infty ;0 \right)\) và \(\left( 2;+\infty \right)\); hàm số nghịch biến trên khoảng \(\left( 0;\ 2 \right).\)
Hàm số đạt cực đại tại \(x=0;\ \ {{y}_{CD}}=5.\)
Hàm số đạt cực tiểu tại \(x=2;\ \ {{y}_{CT}}=1.\)
+) Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ,\mathop {\lim }\limits_{x \to + \infty } y = + \infty \)
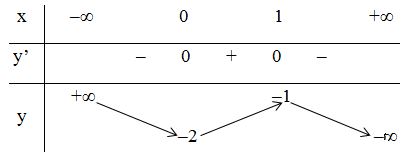
Bảng biến thiên:
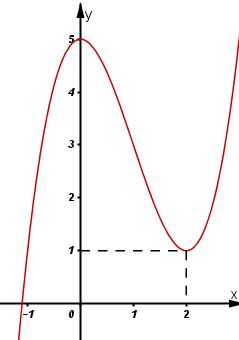
+) Đồ thị hàm số:
Đồ thị hàm số cắt trục \(Oy\) tại điểm \(\left( 0;\ 5 \right).\)
Số nghiệm của phương trình \({{x}^{3}}-3{{x}^{2}}+5=0\) là số giao điểm của đồ thị hàm số \(y={{x}^{3}}-3{{x}^{2}}+5\) và trục hoành.
Từ đồ thị hàm số ta thấy đồ thị hàm số giao với trục hoành tại 1 điểm duy nhất.
Vậy phương trình đã cho có nghiệm duy nhất.
LG b
\(- 2{x^3} + 3{x^2}-2 = 0\) ;
Phương pháp giải:
Xét phương trình tương đương, sau đó:
+) Khảo sát sự biến thiên của các hàm số \(y=f\left( x \right)\) lập bảng biến thiên, vẽ đồ thị hàm số.
+) Số nghiệm của phương trình \(f\left( x \right)=a\) là số giao điểm của đồ thị hàm số \(y=f\left( x \right)\) với đường thẳng \(y=a.\)
+) Khi đó dựa vào đồ thị hàm số để xác định số giao điểm và kết luận.
Lời giải chi tiết:
\(-2{{x}^{3}}+3{{x}^{2}}-2=0.(*)\)
Ta có: (*) \(\Leftrightarrow 2{{x}^{3}}-3{{x}^{2}}=-2.\)
Xét hàm số: \(y=2{{x}^{3}}-3{{x}^{2}}.\)
Tập xác định: \(D=R.\)
Ta có: \(y'=6{{x}^{2}}-6x\) \(\Rightarrow y'=0\Leftrightarrow 6{{x}^{2}}-6x=0\) \(\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=1 \\ \end{align} \right..\)
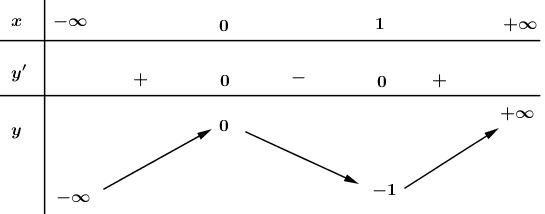
Hàm số đồng biến trên khoảng \(\left( -\infty ;\ 0 \right)\) và \(\left( 1;+\infty \right);\) nghịch biến trên khoảng \(\left( 0;\ 1 \right).\)
Hàm số đạt cực đại tại \(x=0;\ \ {{y}_{CD}}=0.\)
Hàm số đạt cực tiểu tại \(x=1;\ {{y}_{CT}}=-1.\)
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ,\mathop {\lim }\limits_{x \to + \infty } y = + \infty \)
Bảng biến thiên:
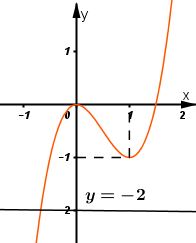
Đồ thị:
Số nghiệm của phương trình \(-2{{x}^{3}}+3{{x}^{2}}-2=0\) là số giao điểm của đồ thị hàm số \(y=2{{x}^{3}}-3{{x}^{2}}\) và đường thẳng \(y=-2.\)
Dựa vào đồ thị hàm số ta thấy đường thẳng \(y=-2\) cắt đồ thị hàm số \(y=2{{x}^{3}}-3{{x}^{2}}\) tại 1 điểm duy nhất.
Vậy phương trình đã cho có nghiệm duy nhất.
Cách khác:
Xét hàm số \(y = {\rm{ }}f\left( x \right) = - 2{x^3}\; + {\rm{ }}3{x^2}-2.\)
- TXĐ: \(D = \mathbb R\)
- Sự biến thiên:
+ Chiều biến thiên:
\(\begin{array}{*{20}{l}}
{y' = - 6{x^2}\; + {\rm{ }}6x = - 6x\left( {x - 1} \right)}\\
{y' = 0{\rm{ }} \Leftrightarrow {\rm{ }}x = 0{\rm{ }};{\rm{ }}x = 1}
\end{array}\)
+ Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = + \infty ,\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = - \infty \)
+ Bảng biến thiên:
- Đồ thị:
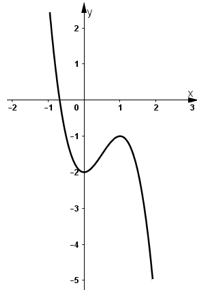
Đồ thị hàm số \(y = f(x)\) cắt trục hoành tại 1 điểm duy nhất
⇒ phương trình \(f(x) = 0)\) có nghiệm duy nhất.
Vậy phương trình \( - 2{x^3}\; + 3{x^2}\; -2 = 0\) chỉ có một nghiệm.
LG c
\(2{x^2}-{x^4} = - 1\).
Phương pháp giải:
+) Khảo sát sự biến thiên của các hàm số \(y=f\left( x \right)\) lập bảng biến thiên, vẽ đồ thị hàm số.
+) Số nghiệm của phương trình \(f\left( x \right)=a\) là số giao điểm của đồ thị hàm số \(y=f\left( x \right)\) với đường thẳng \(y=a.\)
+) Khi đó dựa vào đồ thị hàm số để xác định số giao điểm và kết luận.
Lời giải chi tiết:
\(2{{x}^{2}}-{{x}^{4}}=-1.\)
Xét hàm số: \(y=2{{x}^{2}}-{{x}^{4}}.\)
Tập xác định: \(D=R.\)
Sự biến thiên: \(y'=4x-4{{x}^{3}}\Rightarrow y'=0\) \(\Leftrightarrow 4x-4{{x}^{3}}=0\Leftrightarrow \left[ \begin{align}& x=0 \\ & x=\pm 1 \\ \end{align} \right..\)
Hàm số đồng biến trên khoảng \(\left( -\infty ;\ -1 \right)\) và \(\left( 0;\ 1 \right);\) hàm số nghịch biến trên khoảng \(\left( -1;\ 0 \right)\) và \(\left( 1;+\infty \right).\)
Hàm số đạt cực đại tại hai điểm \(x=-1\) và \(x=1;\ \ {{y}_{CD}}=1.\)
Hàm số đạt cực tiểu tại \(x=0;\ {{y}_{CT}}=0.\)
Giới hạn:\(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ,\mathop {\lim }\limits_{x \to + \infty } y = - \infty \)
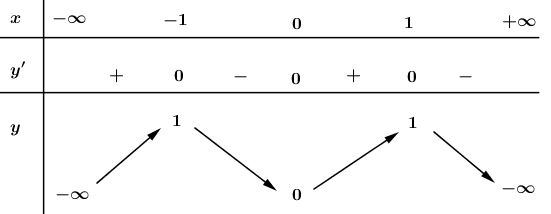
Bảng biến thiên:
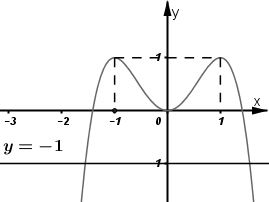
Đồ thị:
Số nghiệm của phương trình \(2{{x}^{2}}-{{x}^{4}}=-1\) là số giao điểm của đồ thị hàm số \(y=2{{x}^{2}}-{{x}^{4}}\) và đường thẳng \(y=-1.\)
Dựa vào đồ thị hàm số ta thấy đường thẳng \(y=-1\) cắt đồ thị hàm số \(y=2{{x}^{2}}-{{x}^{4}}\) tại hai điểm phân biệt.
Vậy phương trình đã cho có 2 nghiệm phân biệt.