Đề bài
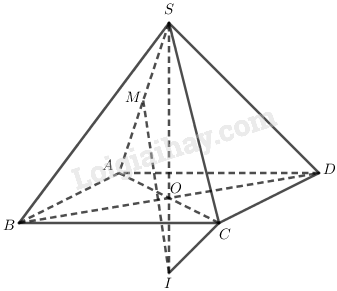
Cho hình vuông \(ABCD\) cạnh \(a\). Từ tâm \(O\) của hình vuông dựng đường thẳng \(\Delta\) vuông góc với mặt phẳng \((ABCD)\). Trên \(\Delta\) lấy điểm \(S\) sao cho \(OS ={a \over 2}\). Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp \(S.ABCD\). Tính diện tích của mặt cầu và thể tích của khối cầu được tạo nên bởi mặt cầu đó.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Nhắc lại: Mặt cầu ngoại tiếp ngoại tiếp hình chóp là mặt cầu đi qua tất cả các đỉnh của chóp.
+) Cách xác định tâm mặt cầu ngoại tiếp:
Bước 1: Xác định trục d của mặt phẳng đáy (là đường thẳng đi qua "tâm đường tròn ngoại tiếp đa giác đáy" và "vuông góc với mp đáy").
Bước 2: Xác định \((P)\): mặt phẳng trung trực của một cạnh bên.
Bước 3: Xác định \(I = \left( P \right) \cap d\), khi đó \(I\) là tâm mặt cầu ngoại tiếp khối chóp.
+) Bán kính \(R\) của mặt cầu: là khoảng cách từ tâm đến 1 đỉnh bất kì.
+) Diện tích mặt cầu \(S = 4\pi {R^2}\)
+) Thể tích khối cầu \(V = \dfrac{4}{3}\pi {R^3}\).
Lời giải chi tiết
* Xác định mặt cầu ngoại tiếp
+ \(\Delta \) là trục của mp đáy
Ta có \(ABCD\) là hình vuông nên \(O\) là tâm đường tròng ngoại tiếp hv \(ABCD\) .
Lại có: \(O \in \Delta ; \Delta \, \bot \, ABCD\)
\(\Rightarrow \Delta \) là trục của mp đáy
+ Xác định tâm \(I\)
Do \(\Delta\) là trục của hình vuông \(ABCD\), nên \(I\) thuộc \(\Delta\).
Ta có: \(ABCD\) là hình vuông cạnh a \( \Rightarrow AC = a\sqrt 2 \Rightarrow OC = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\)
Mà \(SO = \displaystyle {a \over 2} < OC\) nên \(I\) thuộc phần kéo dài của tia \(SO\).
+ Tìm bán kính \(R\)
Ta có: \(SI = IC \Rightarrow \displaystyle {a \over 2} + OI = \sqrt {O{I^2} + O{C^2}} \)
\( \Rightarrow {\left( \displaystyle {{a \over 2} + OI} \right)^2} = O{I^2} +\displaystyle {{{a^2}} \over 2}\)
\( \Rightarrow O{I^2} + a.OI + \displaystyle {{{a^2}} \over 4} = O{I^2} + \displaystyle {{{a^2}} \over 2}\)
\( \Rightarrow OI = \displaystyle {a \over 4} \Rightarrow R = SI = SO + OI = \displaystyle {{3a} \over 4}\)
Vậy tâm \(I\) của mặt cầu ngoại tiếp hình chóp \(S.ABCD\) thuộc tia \(SO\) mà \(SI = R =\) \(\displaystyle {{3a} \over 4}\) ; (\(R\) là bán kính hình cầu).
Khi đó diện tích mặt cầu là: \(S = 4\pi {R^2} = \displaystyle {9 \over 4}\pi {a^2}\) (đvdt)
Thể tích của khối cầu là: \(V = \displaystyle {4 \over 3}\pi {R^3} = \displaystyle {9 \over {16}}{\pi a^3}\) (đvdt)
Cách khác:
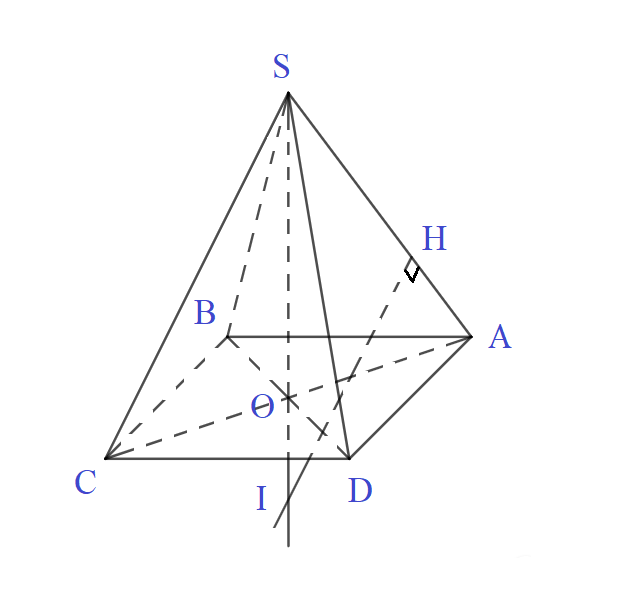
Gọi \(H\) là trung điểm cạnh \(SA\)
Trong mặt phẳng \((SAO)\), đường trung trực của đoạn \(SA\) cắt đường thẳng \(SO\) tại \(I\), ta có:
\(\Delta SAO\) đồng dạng với \(\Delta SIH\)
\( \Rightarrow \dfrac{{SA}}{{SO}} = \dfrac{{SI}}{{SH}} \Leftrightarrow SI = \dfrac{{SA.\,SH}}{{SO}} = \dfrac{{S{A^2}}}{{2\,SO}}\)
Mà \(S{A^2} = S{O^2} + O{A^2}\)
\(\begin{array}{*{20}{l}}
{ \Rightarrow S{A^2} = {{\left( {\dfrac{a}{2}} \right)}^2} + {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2} = \dfrac{{3{a^2}}}{4}}\\
{ \Rightarrow SA = \dfrac{{a\sqrt 3 }}{2}}
\end{array}\)
Khi đó: \(SI = \frac{{\frac{{3{a^2}}}{4}}}{{2.\frac{a}{2}}} = \dfrac{{3a}}{4}\)
Lại có:
\(\left. {\begin{array}{*{20}{l}}
{IS = IA}\\
{IA = IB = IC = ID = \dfrac{{3a}}{4}}
\end{array}} \right\} \Rightarrow IS = \dfrac{{3a}}{4}\)
Vậy mặt cầu ngoại tiếp hình chóp \(S.ABCD\) có tâm là \(I\) và bán kính \(R = IS = \dfrac{{3a}}{4}\)
Diện tích mặt cầu là: \(S = 4\pi {R^2} = 4\pi {\left( {\dfrac{{3a}}{4}} \right)^2} = \dfrac{{9\pi {a^2}}}{4}\)
Thể tích khối cầu là: \(V = \dfrac{4}{3}\pi {R^2} = \dfrac{4}{3}\pi {\left( {\dfrac{{3a}}{4}} \right)^3} = \dfrac{{9\pi {a^2}}}{{16}}\)