Đề bài
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số đã học theo sơ đồ trên
\(y = ax + b\)
\(y = ax^2 + bx + c \)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
B1: Tìm TXĐ
B2: Bảng biến thiên
- Xét chiều biến thiên
+Tính \(y'\).
+ Tìm các điểm mà tại đó hàm số không xác định và nghiệm của \(y'=0\).
+ Xét dấu đạo hàm suy ra chiều biến thiên
- Tìm cực trị
- Tính các giới hạn,tiệm cận (nếu có).
- Lập bảng biến thiên
B3: Vẽ đồ thị
Lời giải chi tiết
* Hàm số \(y = ax + b\)
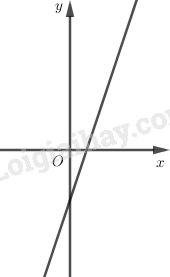
Trường hợp a > 0
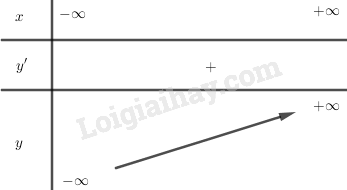
1. TXĐ: \(D = R.\)
2. Sự biến thiên.
\(y’ = a > 0\). Vậy hàm số đồng biến trên toàn bộ R.
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty \cr
& \mathop {\lim }\limits_{x \to - \infty } y = - \infty \cr} \)
Bảng biến thiên
3. Vẽ đồ thị
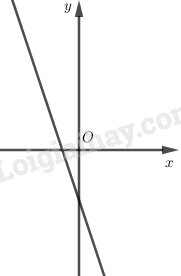
Trường hợp \(a < 0\)
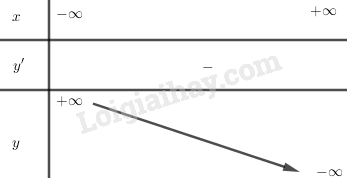
1. TXĐ: \(D = R.\)
2. Sự biến thiên.
\(y’ = a < 0.\) Vậy hàm số đồng biến trên toàn bộ \(R.\)
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = - \infty \cr
& \mathop {\lim }\limits_{x \to - \infty } y = + \infty \cr} \)
Bảng biến thiên
Vẽ đồ thị
* Hàm số \(y = ax^2+ bx + c\)
Trường hợp \(a > 0\)
1. TXĐ: \(D = R.\)
2. Sự biến thiên.
\(y’ = 2ax + b. \)
\(y' = 0 \Rightarrow x = \dfrac { - b} {2a}\)
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty \cr
& \mathop {\lim }\limits_{x \to - \infty } y = + \infty \cr} \)
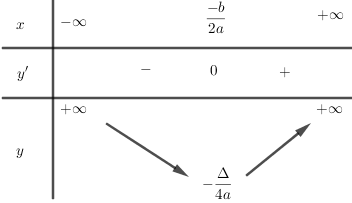
Bảng biến thiên
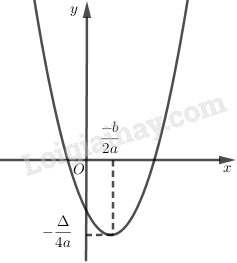
Hàm số nghịch biến trên khoảng (-∞, \({{ - b} \over {2a}}\)).
Hàm số đồng biến trên khoảng (\({{ - b} \over {2a}}\), +∞).
Hàm số đạt cực tiểu bằng \(\dfrac {-\Delta} {4a}\) tại \(x = \dfrac { - b} {2a}\)
Vẽ đồ thị
Trường hợp \(a < 0\)
1. TXĐ: \(D = R.\)
2. Sự biến thiên.
\(y’ = 2ax + b. \)
Cho \(y' = 0 \Rightarrow x = \dfrac { - b} {2a}\)
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = - \infty \cr
& \mathop {\lim }\limits_{x \to + \infty } y = - \infty \cr} \)
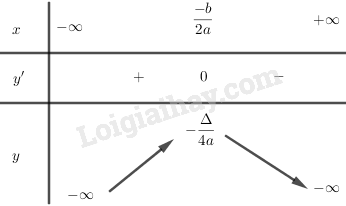
Bảng biến thiên
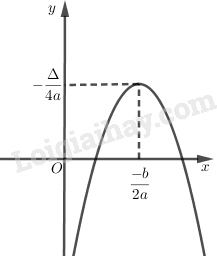
Hàm số đồng biến trên khoảng (-∞, \({{ - b} \over {2a}}\)).
Hàm số nghịch biến trên khoảng \(({{ - b} \over {2a}}, +∞)\).
Hàm số đạt cực đại bằng \( \dfrac {-\Delta} {4a}\) tại \(x = \dfrac { - b} {2a}\)
Vẽ đồ thị