Video hướng dẫn giải
a) Sử dụng đồ thị, hãy xem xét các hàm số sau đây có cực trị hay không
\(y = -2x + 1;\)
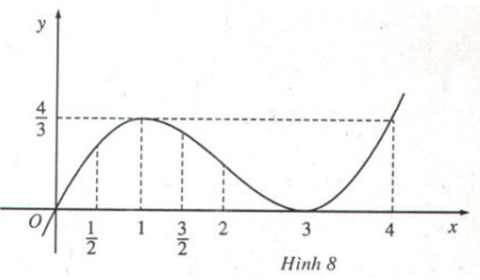
\(y = \dfrac {x{{(x - 3)}^2}} 3\,\,\,(H.8)\)
b) Nêu mối quan hệ giữa sự tồn tại cực trị và dấu của đạo hàm.
LG a
Sử dụng đồ thị, hãy xem xét các hàm số sau đây có cực trị hay không
\(y = -2x + 1;\)
\(y = \dfrac {x{{(x - 3)}^2}} 3\,\,\,(H.8)\)
Phương pháp giải:
Quan sát đồ thị, tìm điểm cực trị ( cực đại: điểm mà tại đó hàm số chuyển từ đồng biến sang nghịch biến, cực tiểu: ngược lại)
Lời giải chi tiết:
Hàm số \(y = -2x + 1\) không có cực trị.
Hàm số \(y = \dfrac {x{{(x - 3)}^2}} 3\) đạt cực đại tại \(x = 1\) và đạt cực tiểu tại \(x = 3.\)
LG b
Nêu mối quan hệ giữa sự tồn tại cực trị và dấu của đạo hàm.
Lời giải chi tiết:
Nếu hàm số có cực trị thì dấu của đạo hàm bên trái và bên phải điểm cực trị sẽ khác nhau.