Video hướng dẫn giải
Trên mặt phẳng toạ độ, tìm tập hợp điểm biểu diễn các số phức zz thoả mãn điều kiện:
LG a
a) |z|=1|z|=1;
Phương pháp giải:
+) Giả sử z=x+yi,(x,y∈R), khi đó trên mặt phẳng toạ độ Oxy, điểm M(x;y) biểu diễn số phức z.
+) |z|=√x2+y2.
+) Phương trình đường thẳng có dạng: ax+by+c=0.
+) Phương trình đường tròn có dạng: (x−a)2+(y−b)2=R2.
Lời giải chi tiết:
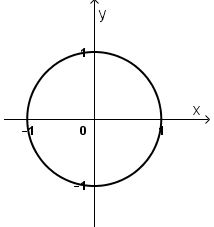
Ta có |z|=1 ⇔√x2+y2=1⇔x2+y2=1.
Vậy tập hợp điểm biểu diễn số phức z là đường tròn tâm O, bán kính bằng 1.
LG b
b) |z|≤1;
Lời giải chi tiết:
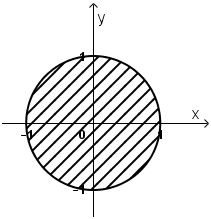
Ta có |z|≤1 ⇔√x2+y2≤1⇔x2+y2≤1.
Vậy tập hợp điểm biểu diễn số phức z là hình tròn tâm O, bán kính bằng 1 (kể cả các điểm trên đường tròn).
LG c
c) 1<|z|≤2;
Lời giải chi tiết:
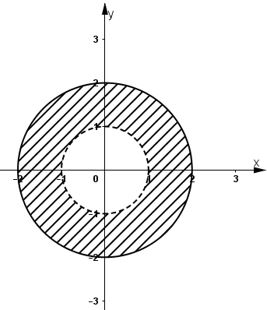
Ta có 1<|z|≤2 ⇔1<√x2+y2≤2 ⇔1<x2+y2≤4.
Vậy tập hợp điểm biểu diễn số phức z là phần nằm giữa đường tròn tâm O, bán kính bằng 1 (không kể điểm trên đường tròn này) và đường tròn tâm O, bán kính bằng 2 (kể cả các điểm trên đường tròn này).
LG d
d) |z|=1 và phần ảo của z bằng 1.
Lời giải chi tiết:
Ta có |z|=1 ⇔√x2+y2=1 ⇔x2+y2=1 và phần ảo của z bằng 1 tức y=1. Suy ra x=0 và y=1.
Vậy tập hợp các điểm cần tìm là điểm A(0;1).
