Đề bài
Gọi \(S\) là diện tích xung quanh của hình nón tròn xoay được sinh ra bởi đoạn thẳng \(AC'\) của hình lập phương \(ABCD.A'B'C'D'\) có cạnh \(b\) khi quay xung quanh trục \(AA'\). Diện tích \(S\) là:
(A) \(πb^2\); (B) \(πb^2\sqrt 2 \) ;
(C) \(πb^2\sqrt 3 \) ; (D) \(πb^2\sqrt 6 \).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Khi quay \(AC'\) xung quanh trục \(AA'\) ta được hình nón đỉnh A có chiều cao \(AA'\), đường sinh \(AC'\) và bán kính đáy \(A'C'\).
Công thức tính diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl\), trong đó \(r;l\) lần lượt là bán kính đáy và độ dài đường sinh của hình nón.
Lời giải chi tiết
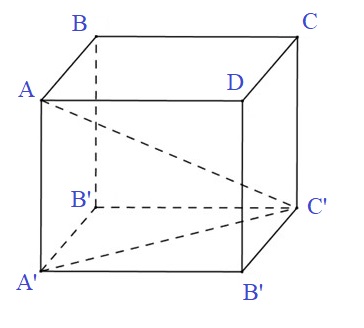
Hình nón tạo bởi khi quay \(AC'\) xung quanh \(AA'\) có đường sinh \(l=AC'\) và bán kính đáy \(r=C'A'\)
Xét tam giác vuông \(A'B'C'\) có: \(A'C' = \sqrt {A'B{'^2} + B'C{'^2}} = \sqrt {{b^2} + {b^2}} = b\sqrt 2=r \)
Xét tam giác vuông \(AA'C'\) có: \(AC' = \sqrt {AA{'^2} + A'C{'^2}} = \sqrt {{b^2} + 2{b^2}} = b\sqrt 3=l \)
Vậy \({S_{xq}} = \pi rl = \pi b\sqrt 2 .b\sqrt 3 = \pi {b^2}\sqrt 6 \)
Chọn (D).

