Đề bài
Cho hình lập phương \(ABCD.A’B’C’D’\) cạnh \(a\). Tính diện tích xung quanh của hình trụ và thể tích của khối trụ có hai đáy là hai hình tròn ngoại tiếp hai hình vuông \(ABCD\) và \(A’B’C’D’\).
Video hướng dẫn giải
Lời giải chi tiết
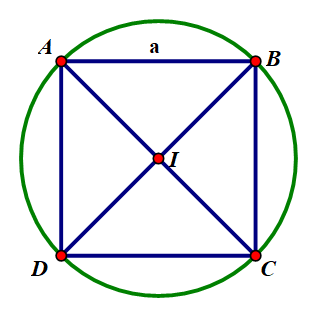
Biểu diễn đường tròn ngoại tiếp hình vuông \(ABCD\) cạnh \(a\) như hình vẽ
Khi đó: Tâm đường tròn là giao điểm 2 đường chéo.
Bán kính đường tròn \(= r = IA = {{a\sqrt 2 } \over 2}\)
Diện tích đường tròn là: \(\pi {r^2} = {{{\pi a^2}} \over 2}\)
\( \Rightarrow \) Diện tích xung quanh của hình trụ thỏa mãn đề bài \((l = a)\) là:
\({S_{xq}} = 2\pi rl = 2\pi a{{\sqrt 2 } \over 2}a = \pi {a^2}{{\sqrt 2 }}\)
Diện tích khối trụ thỏa mãn đề bài \((h = a)\) là:
\(V = B.h = {{{\pi a^2}} \over 2}a = {{{\pi a^3}} \over 2}\)