Đề bài
Tìm tập hợp tất cả các điểm trong không gian luôn luôn nhìn đoạn thẳng \(AB\) cố định dưới một góc vuông.
Phương pháp giải - Xem chi tiết
+) Trong tam giác vuông có đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
+) Tâm đường tròn ngoại tiếp tam giác tam giác vuông là trung điểm của cạnh huyền.
Lời giải chi tiết
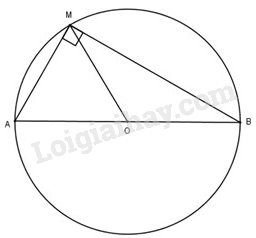
Gọi \(O\) là trung điểm đoạn thẳng \(AB\), vì tam giác \(AMB\) vuông tại \(M\) nên trung tuyến \(MO\) bằng nửa cạnh huyền, tức \(MO = {AB\over2} = R\).
Vậy tập hợp các điểm \(M\) nhìn \(AB\) dưới một góc vuông nằm trên mặt cầu đường kính \(AB\)
Ngược lại, lấy \(M\) thuốc mặt cầu đường kính \(AB\) thì \(MO = {AB\over2}\).
Do đó nếu \(M\) khác \(A\) và \(B\) thì tam giác \(MAB\) vuông tại \(M\), còn khi \(M \equiv A\) hoặc \(M \equiv B\) ta cũng coi \(M\) nhìn \(AB\) một góc vuông.
Kết luận: Tập hợp các điểm \(M\) trong không gian nhìn đoạn thẳng \(AB\) dưới một góc vuông là mặt cầu đường kính \(AB\).