Đề bài
Lập bảng biến thiên của hàm số \(\displaystyle f(x) = -{{ 1} \over {1 + {x^2}}}\)
Từ đó suy ra giá trị nhỏ nhất của \(f(x)\) trên tập xác định.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Tìm tập xác định của hàm số.
+) Tính đạo hàm của hàm số. Tìm các điểm \(x_i \,(i =1,2,3,…,n)\) mà tại đó đạo hàm bằng 0 hoặc không xác định
+) Sắp xếp các điểm \(x_i\) theo thứ tự tăng dần và lập bảng biến thiên
+) Dựa vào bảng biến thiên, khoảng đồng biến và nghịch biến của hàm số trên tập xác định của nó để suy ra GTNN
Lời giải chi tiết
1. TXĐ: \(D = \mathbb R.\)
2. \(y' =\dfrac {2x} {{(1 + {x^2})}^2}\)
Cho \(y’ = 0\) thì \(x = 0\).
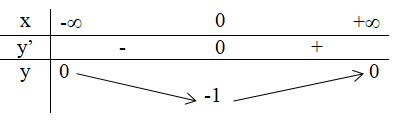
3. Bảng biến thiên
Vậy giá trị nhỏ nhất của hàm số đã cho là \(– 1\) tại \(x = 0\).