Video hướng dẫn giải
Giải các bất phương trình
LG a
a) \({2^{2x - 1}} + {\rm{ }}2{^{2x - 2}} + {\rm{ }}{2^{2x - 3}} \ge {\rm{ }}448\)
Phương pháp giải:
Đặt nhân tử chung \(2^{2x-3}\), đưa bất phương trình mũ về dạng cơ bản:
\({a^x} \ge b \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a > 1\\x \ge {\log _a}b\end{array} \right.\\\left\{ \begin{array}{l}0 < a < 1\\x \le {\log _a}b\end{array} \right.\end{array} \right.\)
Lời giải chi tiết:
\(\displaystyle \begin{array}{l}a)\,\,\,{2^{2x - 1}} + {2^{2x - 2}} + {2^{2x - 3}} \ge 448\\\Leftrightarrow {2^{2x - 3}}{.2^2} + {2^{2x - 3}}{.2^1} + {2^{2x - 3}} \ge 448\\\Leftrightarrow {2^{2x - 3}}\left( {4 + 2 + 1} \right) \ge 448\\\Leftrightarrow {7.2^{2x - 3}} \ge 448\\\Leftrightarrow {2^{2x - 3}} \ge 64\\\Leftrightarrow 2x - 3 \ge {\log _2}64 = 6\\\Leftrightarrow x \ge \dfrac{9}{2}\end{array}\)
Vậy tập nghiệm của bất phương trình đã cho là: \(\displaystyle S=\left[{{9}\over {2}}; +∞\right)\).
LG b
b) \({\left( {0,4} \right)^x}-{\rm{ }}{\left( {2,5} \right)^{x + 1}} > {\rm{ }}1,5\)
Phương pháp giải:
Đặt ẩn phụ \(t = {\left( {0,4} \right)^x}\), để ý rằng: \(0,4.2,5 = 1 \Rightarrow {\left( {0,4} \right)^x}.{\left( {2,5} \right)^x} = 1\) \(\Rightarrow {\left( {2,5} \right)^x} = \dfrac{1}{{{{\left( {0,4} \right)}^x}}}\)
Lời giải chi tiết:
\(\displaystyle \begin{array}{l}\,\,{\left( {0,4} \right)^x} - {\left( {2,5} \right)^{x + 1}} > 1,5\\\Leftrightarrow {\left( {0,4} \right)^x} - 2,5.{\left( {2,5} \right)^x} > 1,5\\\Leftrightarrow {\left( {0,4} \right)^x} - 2,5.\dfrac{1}{{{{\left( {0,4} \right)}^x}}} > 1,5\end{array}\)
Đặt \(\displaystyle t = {(0,4)}^x> 0\), bất phương trình đã cho trở thành:
\(\displaystyle \eqalign{
& t - {{2,5} \over t} > 1,5 \cr & \Leftrightarrow {t^2} - 1,5t - 2,5 = 0\cr &\Leftrightarrow 2{t^2} - 3t - 5 > 0 \cr
& \Leftrightarrow \left[ \matrix{
t < - 1 \hfill \cr
t > 2,5 \hfill \cr} \right. \cr} \)
Do \(\displaystyle t = {(0,4)}^x> 0\), bất phương trình đã cho tương đương với:
\(\displaystyle {\left( {0,4} \right)^x} > {\rm{ }}2,5{\rm{ }} \Leftrightarrow {\rm{ }}{\left( {0,4} \right)^x} > {\rm{ }}{\left( {0,4} \right)^{ - 1}} \) \(\Leftrightarrow {\rm{ }}x{\rm{ }} < {\rm{ }} - 1\)
Vậy tập nghiệm của bất phương trình là \(\displaystyle S = \left( { - \infty ; - 1} \right)\).
Cách trình bày khác:
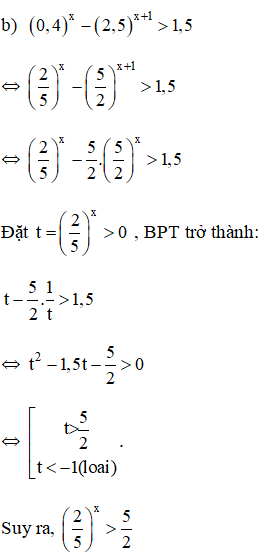
\( \Leftrightarrow {\left( {\dfrac{2}{5}} \right)^x} > {\left( {\dfrac{2}{5}} \right)^{ - 1}}\)
Vậy tập nghiệm của bất phương trình là \(\displaystyle S = \left( { - \infty ; - 1} \right)\).
LG c
c) \({\log _3}\left[ {{{\log }_{{1 \over 2}}}({x^2} - 1)} \right] < 1\)
Phương pháp giải:
Giải bất phương trình logarit cơ bản:
\({\log _a}f\left( x \right) < b \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a > 1\\f\left( x \right) < {a^b}\end{array} \right.\\\left\{ \begin{array}{l}0 < a < 1\\f\left( x \right) > {a^b}\end{array} \right.\end{array} \right.\)
Lời giải chi tiết:
ĐK: \(\displaystyle \left\{ \begin{array}{l}{\log _{\frac{1}{2}}}\left( {{x^2} - 1} \right) > 0\\{x^2} - 1 > 0\end{array} \right. \) \(\displaystyle \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 1 < {\left( {\dfrac{1}{2}} \right)^0} = 1\\{x^2} - 1 > 0\end{array} \right.\) \(\displaystyle \Leftrightarrow \left\{ \begin{array}{l}- \sqrt 2 < x < \sqrt 2 \\\left[ \begin{array}{l}x > 1\\x < - 1\end{array} \right.\end{array} \right.\) \(\displaystyle \Leftrightarrow x \in \left( { - \sqrt 2 ;-1} \right) \cup \left( {1;\sqrt 2 } \right)\)
Ta có:
\(\displaystyle \begin{array}{l}\,\,\,\,\,{\log _3}\left[ {{{\log }_{\frac{1}{2}}}\left( {{x^2} - 1} \right)} \right] < 1\\\Leftrightarrow 0< {\log _{\frac{1}{2}}}\left( {{x^2} - 1} \right) < {3^1} = 3\\\left( {Do\,3 > 1} \right)\\\Leftrightarrow {\left( {\dfrac{1}{2}} \right)^0} > {x^2} - 1 > {\left( {\dfrac{1}{2}} \right)^3} = \dfrac{1}{8}\\ \left( {Do\,\,0 < \,\dfrac{1}{2} < 1} \right)\\\Leftrightarrow 2 > {x^2} > \dfrac{9}{8}\end{array}\)
\(\begin{array}{l}
\Leftrightarrow \left\{ \begin{array}{l}
{x^2} < 2\\
{x^2} > \dfrac{9}{8}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
- \sqrt 2 < x < \sqrt 2 \\
\left[ \begin{array}{l}
x > \dfrac{3}{{2\sqrt 2 }}\\
x < - \dfrac{3}{{2\sqrt 2 }}
\end{array} \right.
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
\dfrac{3}{{2\sqrt 2 }} < x < \sqrt 2 \\
- \sqrt 2 < x < - \dfrac{3}{{2\sqrt 2 }}
\end{array} \right.
\end{array}\)
Kết hợp điều kiện ta có: \(\displaystyle x \in \left( { - \sqrt 2 ; - \dfrac{3}{{2\sqrt 2 }}} \right) \cup \left( {\dfrac{3}{{2\sqrt 2 }};\sqrt 2 } \right)\)
Vậy tập nghiệm của bất phương trình là: \(\displaystyle S = \left( { - \sqrt 2 ; - \dfrac{3}{{2\sqrt 2 }}} \right) \cup \left( {\dfrac{3}{{2\sqrt 2 }};\sqrt 2 } \right)\).
LG d
d) \({\log _{0,2}}^2x - 5.{\log _{0,2}}x < - 6\)
Phương pháp giải:
Đặt ẩn phụ \(t = {\log _{0,2}}x\).
Lời giải chi tiết:
\(\displaystyle {\log _{0,2}}^2x - 5.{\log _{0,2}}x < - 6\)
ĐK: \(\displaystyle x>0\).
Đặt \(\displaystyle t{\rm{ }} = {\rm{ }}{\log_{0,2}}x\). Bất phương trình trở thành
\(\displaystyle {t^2}-{\rm{ }}5t{\rm{ }} + {\rm{ }}6{\rm{ }} < {\rm{ }}0{\rm{ }} \Leftrightarrow {\rm{ }}2{\rm{ }} < {\rm{ }}t{\rm{ }} < {\rm{ }}3\)
Suy ra: \(\displaystyle 2 < {\log _{0,2}}x < 3 \Leftrightarrow {(0,2)^3} < x < {(0,2)^2}\) \(\displaystyle \Leftrightarrow {1 \over {125}} < x < {1 \over {25}}(tm \,\, x>0) \)
Vậy tập nghiệm của bất phương trình là \(\displaystyle S=\left({1 \over {125}},{1 \over {25}}\right)\)

