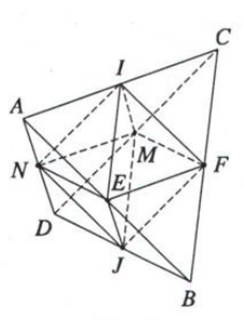
Đề bài
Chứng minh rằng tam giác \(IEF, IFM, IMN, INE, JEF, JFM, JMN\) và \(JNE\) là những tam giác đều cạnh bằng \( \dfrac a 2\)
Video hướng dẫn giải
Lời giải chi tiết
\(ABCD\) là tứ diện đều ⇒ tam giác \(ABC\) đều \(⇒ AB = BC = CA = a\)
\(I, E, F\) lần lượt là trung điểm của các cạnh \(AC, AB, BC\) nên ta có \(IE, IF, EF\) là các đường trung bình của tam giác \(ABC\)
\(\eqalign{
& \Rightarrow IE = {1 \over 2}BC = {1 \over 2}a \cr
& {\rm{IF = }}{1 \over 2}AB = {1 \over 2}a \cr
& {\rm{EF = }}{1 \over 2}AC = {1 \over 2}a \cr} \)
Nên tam giác \(IEF\) là tam giác đều cạnh bằng \(\dfrac a 2\)
Chứng minh tương tự ta có:\(IFM, IMN, INE, JEF, JFM, JMN\) và \(JNE\) là những tam giác đều cạnh bằng \(\dfrac a 2\)