1. Kiến thức cần nhớ
a) Định nghĩa Acgumen của số phức.
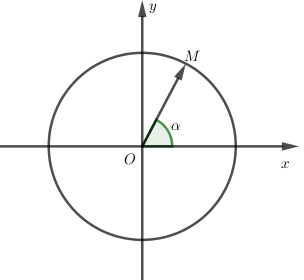
- Điểm M≠O biểu diễn số phức z=a+bi(a,b∈R) thì số đo mỗi góc lượng giác tia đầu là Ox và tia cuối OM được gọi là acgumen của số phức z.
- Nếu α là một acgumen của z thì α+k2π cũng là một acgumen của z với mỗi k∈Z.
b) Khái niệm về dạng lượng giác của số phức
- Số phức z=a+bi là dạng đại số của z.
- Số phức z=r(cosφ+isinφ) là dạng lượng giác của z, ở đó:
+ r là mô đun của số phức.
+ φ là acgumen của số phức.
c) Các phép toán với số phức dạng lượng giác:
Cho hai số phức z1=r1(cosφ1+isinφ1),z2=r2(cosφ2+isinφ2). Khi đó:
z1±z2=r1(cosφ1+isinφ1)±r2(cosφ2+isinφ2)=(r1cosφ1±r2cosφ2)+i(r1sinφ1±r2sinφ2)z1.z2=r1(cosφ1+isinφ1).r2(cosφ2+isinφ2)=r1r2[cos(φ1+φ2)+isin(φ1+φ2)]z1z2=r1(cosφ1+isinφ1)r2(cosφ2+isinφ2)=r1r2[cos(φ1−φ2)+isin(φ1−φ2)]
d) Công thức Moivre:
Cho số phức z=r(cosφ+isinφ). Khi đó:
zn=[r(cosφ+isinφ)]n=rn(cosnφ+isinnφ)
2. Một số dạng toán thường gặp
Dạng 1: Chuyển số phức từ dạng đại số sang dạng lượng giác.
Cho số phức z=a+bi, viết z dưới dạng z=r(cosφ+isinφ)
Phương pháp:
- Bước 1: Tính r=√a2+b2
- Bước 2: Tính φ thỏa mãn {cosφ=arsinφ=br
Dạng 2: Tính giá trị, rút gọn biểu thức.
Phương pháp:
Sử dụng các phép toán cộng, trừ, nhân, chia số phức, công thức Moivre để tính giá trị và rút gọn các biểu thức.
