Đề bài
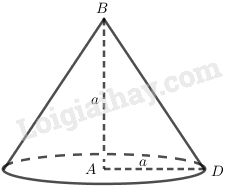
Cho tứ diện \(ABCD\) có cạnh \(AD\) vuông góc với mặt phẳng \((ABC)\) và cạnh \(BD\) vuông góc với cạnh \(BC\). Biết \(AB = AD = a\), tính diện tích xung quanh và thể tích của khối nón được tạo thành khi quay đường gấp khúc \(BDA\) quanh cạnh \(AB\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Vì \(∆ABD\) vuông góc tại \(A\), nên khi quay \(BDA\) quanh \(AB\) ta được hình nón tròn xoay đường cao \(h=AB \) và bán kính đáy bằng \(r=AD.\)
Sử dụng công thức tính diện tích xung quanh và thể tích khối nón: \({S_{xq}} = \pi rl,\,\,V = \dfrac{1}{3}\pi {r^2}h\)
Lời giải chi tiết
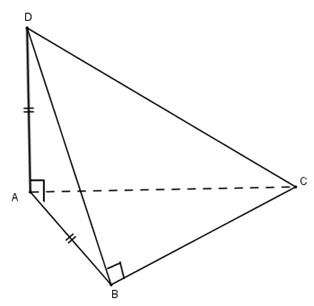
\(AD \bot \left( {ABC} \right) \Rightarrow AD \bot AB \Rightarrow \Delta ABD\) vuông tại A.
Vì \(∆ABD\) vuông góc tại \(A\), nên khi quay \(BDA\) quanh \(AB\) ta được hình nón tròn xoay đường cao \(h=AB = a\) và bán kính đáy bằng \(r=AD =a\).
Gọi \(l\) là độ dài đường sinh của hình nón ta có: \(l = \sqrt {{r^2} + {h^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
Vậy \({S_{xq}} = \pi rl = \pi .a.a\sqrt 2 = \pi {a^2}\sqrt 2 ,\) \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi .{a^2}.a = \dfrac{{\pi {a^3}}}{3}\)