Đề bài
Tìm tập hợp tâm những mặt cầu luôn cùng tiếp xúc với ba cạnh của một tam giác cho trước.
Lời giải chi tiết
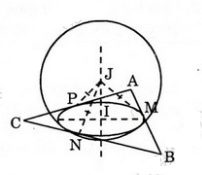
* Lấy một mặt cầu bất kì (S) thỏa mãn ycđb.
Giả sử (S) có tâm J, bán kính R và tiếp xúc với ba cạnh: \(AB, BC, AC\) lần lượt tại \(M, N và P\).
Gọi I là hình chiếu vuông góc của J lên mp \((ABC) ⇒ IJ ⊥ (ABC)\). Ta sẽ chứng minh I là tâm đường tròn nội tiếp tam giác ABC.
* Ta có: \(\left\{ \begin{array}{l}JM \bot AB\\JI \bot AB\end{array} \right. \Rightarrow IM \bot AB\) (định lí 3 đường vuông góc)
Chứng minh tương tự có:\(IN \bot BC,IP \bot AC\) (1)
* Xét ba tam giác \( JIM; JIN và JIP\) có:
\(\widehat {JIM} = \widehat {JIN} = \widehat {JIP} = {90^0}\)
\(JI\) chung
\(JN = JM = JP = R\)
⇒ \(∆ JIM = ∆ JIN = ∆JIP\) (ch- cgv)
⇒ \(IN = IM = IP\) (2)
Từ (1) và (2) suy ra, I là tâm đường tròn nội tiếp tam giác ABC.
Vậy J thuộc đường thẳng d qua I, vuông góc với mp (ABC)
* Ngược lại lấy điểm J bất kì thuộc d, ta chứng minh tồn tại mặt cầu tâm J tiếp xúc với 3 cạnh của tam giác ABC.
Gọi \(M, N và P\) lần lượt là hình chiếu của I xuống 3 cạnh \(AB, BC và CA\)
Ta có: \(\left\{ \begin{array}{l}IM \bot AB\\JI \bot AB\end{array} \right. \Rightarrow JM \bot AB\)
\(JN \bot BC,JP \bot AC\) (1)
Mặt khác; \(IM = IN = IP = r\).
⇒ \(∆ JIM = ∆ JIN = ∆JIP\) (c-g-c)
⇒ \(JM = JN = JP\) (2)
Từ (1) và (2) suy ra, mặt cầu (S) tâm J, bán kính JM tiếp xúc với ba cạnh của tam giác ABC.
Vậy tập hợp tâm các mặt cầu tiếp xúc với ba cạnh của tam giác ABC cho trước là đường thẳng d đi qua tâm đường tròn ngoại tiếp của ∆ABC và vuống góc với mp (ABC)

