Video hướng dẫn giải
LG a
Xét các hàm số sau và đồ thị của chúng:
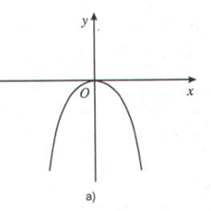
\(\displaystyle y\, = \,{{ - {x^2}} \over 2}\) (H.4a)
Xét dấu đạo hàm của hàm số và điền vào bảng tương ứng.
Phương pháp giải:
Quan sát đồ thị, nhận xét khoảng đồ thị đi lên (đồng biến) hay đi xuống (nghịch biến), từ đó suy ra dấu của đạo hàm:
Trên từng khoảng, nếu đồ thị hàm số đi lên (từ trái qua phải) thì hàm số đồng biến trên khoảng đó, đồng thời đạo hàm mang dấu (+) trên khoảng đó.
Ngược lại, nếu đồ thị hàm số đi xuống(từ trái qua phải) thì hàm số nghịch biến trên khoảng đó, đồng thời đạo hàm mang dấu (-) trên khoảng ấy.
Lời giải chi tiết:
Quan sát đồ thị, dễ thấy:
- Trên khoảng \(\left( { - \infty ;0} \right)\): đồ thị hàm số đi lên (từ trái qua phải) nên hàm số đồng biến trên \(\left( { - \infty ;0} \right)\), và \(y' > 0,\forall x \in \left( { - \infty ;0} \right)\).
- Trên khoảng \(\left( 0;{ + \infty }\right)\), đồ thị hàm số đi xuống (từ trái qua phải) nên hàm số nghịch biến trên \(\left( 0;{ + \infty }\right)\), và \(y' < 0,\forall x \in \left( 0;{ + \infty }\right)\).
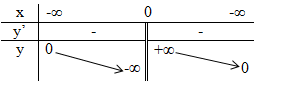
Bảng xét dấu:
LG b
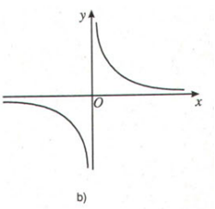
\(\displaystyle y\, = \,{1 \over x}\) (H.4b)
Xét dấu đạo hàm của hàm số và điền vào bảng tương ứng.
Phương pháp giải:
Quan sát đồ thị, nhận xét khoảng đồ thị đi lên (đồng biến) hay đi xuống (nghịch biến), từ đó suy ra dấu của đạo hàm:
Trên từng khoảng, nếu đồ thị hàm số đi lên (từ trái qua phải) thì hàm số đồng biến trên khoảng đó, đồng thời đạo hàm mang dấu (+) trên khoảng đó.
Ngược lại, nếu đồ thị hàm số đi xuống(từ trái qua phải) thì hàm số nghịch biến trên khoảng đó, đồng thời đạo hàm mang dấu (-) trên khoảng ấy.
Lời giải chi tiết:
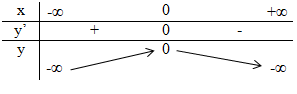
Quan sát đồ thị ta thấy:
- Tại \(x=0\) thì không có giá trị của \(y\) nên hàm số không xác định tại \(x=0\)
- Trên mỗi khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\) thì đồ thị đi xuống (từ trái qua phải) nên hàm số nghịch biến trên mỗi khoảng này.
Khi đó \(y' < 0,\forall x \in \left( { - \infty ;0} \right)\) và \(y' < 0,\forall x \in \left( {0; + \infty } \right)\)
Bảng xét dấu: