Video hướng dẫn giải
Trong mỗi trường hợp sau đây, hãy gọi tên các hình tròn xoay hoặc khối tròn xoay sinh ra bởi:
LG a
a) Ba cạnh của hình chữ nhật khi quay quanh đường thẳng chứa cạnh thứ tư.
Phương pháp giải:
Dựa vào định nghĩa mặt tròn xoay: Mặt trụ và mặt nón.
Lời giải chi tiết:
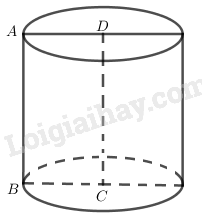
Khi xoay ba cạnh của hình chữ nhật khi quay quanh đường thẳng chứa cạnh thứ tư ta được hình trụ tròn xoay có đường cao là cạnh thứ tư còn bán kính hình trụ bằng độ dài của cạnh kề với cạnh thứ tư đó.
Ví dụ khi xoay ba cạnh của hình chữ nhật \(ABCD\) quanh cạnh \(CD\) ta đươc hình trụ tròn xoay có đường cao \(CD\) và bán kính đáy \(AD\).
LG b
b) Ba cạnh của một tam giác cân khi quay quanh trục đối xứng nó.
Phương pháp giải:
Dựa vào định nghĩa mặt tròn xoay: Mặt trụ và mặt nón.
Lời giải chi tiết:
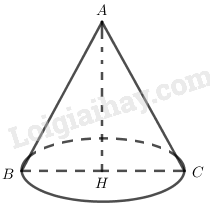
Khi xoay ba cạnh của một tam giác cân khi quay quanh trục đối xứng nó ta được hình nón tròn xoay có chiều cao bằng chiều cao của tam giác cân, còn bán kính đáy bằng một nửa độ dài cạnh đáy của tam giác cân đó.
Ví dụ: Tam giác \(ABC\) cân tại \(A\) có trục đối xứng \(AH\). Khi quay tam giác \(ABC\) quanh \(AH\) ta được hình nón có đường cao \(AH\) và bán kính đáy bằng \(\frac{{BC}}{2}\).
LG c
c) Một tam giác vuông kể cả các điểm trong của tam giác vuông đó khi quay quanh đường thẳng chứa một cạnh góc vuông.
Phương pháp giải:
Dựa vào định nghĩa mặt tròn xoay: Mặt trụ và mặt nón.
Lời giải chi tiết:
Khi xoay một tam giác vuông kể cả các điểm trong của tam giác vuông đó khi quay quanh đường thẳng chứa một cạnh góc vuông ta được khối nón tròn xoay.
LG d
d) Một hình chữ nhật kể cả các điểm trong của hình chữ nhật đó khi quay quanh đường thẳng chứa một cạnh.
Phương pháp giải:
Dựa vào định nghĩa mặt tròn xoay: Mặt trụ và mặt nón.
Lời giải chi tiết:
Khi xoay một hình chữ nhật kể cả các điểm trong của hình chữ nhật đó khi quay quanh đường thẳng chứa một cạnh ta được khối trụ tròn xoay.