Đề bài
Câu 1 Tìm tất cả các giá trị thực của m để đường thẳng \(y = x + m - 1\) cắt đồ thị hàm số \(y = \dfrac{{2x + 1}}{{x + 1}}\) tại hai điểm phân biệt A, B sao cho \(AB = 2\sqrt 3 \)
A. \(m = 2 \pm \sqrt 3 \)
B. \(m = 4 \pm \sqrt 3 \)
C. \(m = 2 \pm \sqrt {10} \)
D. \(m = 4 \pm \sqrt {10} \)
Câu 2. Tính tổng tất cả các nghiệm của phương trình \({e^{\sin \left( {x - \dfrac{\pi }{4}} \right)}} = \tan x\) thuộc đoạn \(\left[ {0;50\pi } \right]\) ?
A. \(\dfrac{{2105\pi }}{2}\)
B. \(\dfrac{{1853\pi }}{2}\)
C. \(\dfrac{{2475\pi }}{2}\)
D. \(\dfrac{{2671\pi }}{2}\)
Câu 3. Cho hình chóp S.ABCD có \(SA \bot \left( {ABCD} \right),\,\,AC = a\sqrt 2 ,\,\,{S_{ABCD}} = \dfrac{{3{a^2}}}{2}\) và góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 600. Gọi H là hình chiếu vuông góc của A trên SC. Tính theo a thể tích khối chóp H.ABCD.
A. \(\dfrac{{{a^3}\sqrt 6 }}{4}\)
B. \(\dfrac{{{a^3}\sqrt 6 }}{2}\)
C. \(\dfrac{{{a^3}\sqrt 6 }}{8}\)
D. \(\dfrac{{3{a^3}\sqrt 6 }}{4}\)
Câu 4. Số nghiệm của phương trình \(\cos x = \dfrac{1}{2}\) thuộc đoạn \(\left[ { - 2\pi ;2\pi } \right]\) là:
A. 1 B. 4
C. 2 D. 3
Câu 5. Trong dãy số \(\left( {{u_n}} \right)\) cho dưới đây, dãy số nào có giới hạn khác 1?
A. \(\left\{ \begin{array}{l}{u_1} = 2018\\{u_{n + 1}} = \dfrac{1}{2}\left( {{u_n} + 1} \right),\,\,n \ge 1\end{array} \right.\)
B. \({u_n} = n\left( {\sqrt {{n^2} + 2020} - \sqrt {4{n^2} + 2017} } \right)\)
C. \({u_n} = \dfrac{1}{{1.3}} + \dfrac{1}{{3.5}} + ... + \dfrac{1}{{\left( {2n + 1} \right)\left( {2n + 3} \right)}}\)
D. \({u_n} = \dfrac{{n{{\left( {n - 2018} \right)}^{2017}}}}{{{{\left( {n - 2017} \right)}^{2018}}}}\)
Câu 6. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để điểm cực tiểu của đồ thị hàm số \(y = {x^3} + {x^2} + mx - 1\) nằm bên phải trục tung. Tìm số phần tử của tập hợp \(\left( { - 5;6} \right) \cap S\) .
A.5 B. 3
C. 2 D. 1
Câu 7. Tâm các mặt hình lập phương tạo thành các đỉnh của khối đa diện nào sau đây?
A. Khối chóp lục giác đều
B. Khối bát diện đều
C. Khối lăng trụ tam giác đều
D. Khối tứ diện đều.
Câu 8. Có bao nhiêu phép tịnh tiến biến một đường tròn thành chính nó?
A. 3 B. 0
C. 2 D. 1
Câu 9. Trong mặt phẳng (P) cho tam giác OAB cân tại O, \(OA = OB = 2a,\,\,\widehat {AOB} = {120^0}.\) Trên đường thẳng vuông góc với mặt phẳng (P) tại O lấy hai điểm C, D nằm về hai phía của mặt phẳng (P) sao cho tam giác ABC vuông tại C và tam giác ABD đều. Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD.
A. \(\dfrac{{3a\sqrt 2 }}{2}\)
B. \(\dfrac{{a\sqrt 2 }}{3}\)
C. \(\dfrac{{5a\sqrt 2 }}{2}\)
D. \(\dfrac{{5a\sqrt 2 }}{3}\)
Câu 10. Cho hình nón S có bán kính \(R = a\sqrt 2 \) , góc ở đỉnh bằng 600. Diện tích xung quanh của hình nón bằng :
A. \(\pi {a^2}\)
B. \(6\pi {a^2}\)
C. \(2\pi {a^2}\)
D. \(4\pi {a^2}\)
Câu 11. Tìm hệ số của x4 trong khai triển nhị thức Newton \({\left( {2x + \dfrac{1}{{\sqrt[5]{x}}}} \right)^n}\), biết n là số tự nhiên lớn nhất thỏa mãn \(A_n^5 \le 18A_{n - 2}^4\)
A. 8064
B. 3360
C. 15360
D. 13440
Câu 12. Xét các mệnh đề sau trong không gian, hỏi mệnh đề nào sai?
A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
B. Mặt phẳng (P) và đường thẳng a không nằm trên (P) cùng vuông góc với đường thẳng b thì song song với nhau.
C. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
D. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
Câu 13. Trong không gian với hệ tọa độ Oxtz, cho bốn vector \(\overrightarrow a = \left( {2;3;1} \right),\,\,\overrightarrow b = 5;7;0;\,\,\overrightarrow c = \left( {3; - 2;4} \right)\) và \(\overrightarrow d = \left( {4;12; - 3} \right)\). Mệnh đề nào sau đây sai?
A. \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) là ba vector không đồng phẳng
B. \(2\overrightarrow a + 3\overrightarrow b = \overrightarrow d - 2\overrightarrow c \)
C. \(\overrightarrow d = \overrightarrow a + \overrightarrow b - \overrightarrow c \)
D. \(\left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow d + \overrightarrow c } \right|\)
Câu 14. Từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9 có thể lập được bao nhiêu số tự nhiên có hai chữ số mà chữ số hàng đơn vị lớn hơn chữ số hàng chục.
A. 36 B. 54
C. 48 D. 72
Câu 15. Các nghiệm của phương trình \(2\left( {1 + \cos x} \right)\left( {1 + {{\cot }^2}x} \right) = \dfrac{{\sin x - 1}}{{\sin x + \cos x}}\) được biểu diễn với bao nhiêu điểm trên đường tròn lượng giác ?
A. 1 B. 4
C. 2 D. 3
Câu 16. Từ một hộp chứa 6 quả cầu đỏ và 4 quả cầu xanh, lấy ngẫu nhiên đồng thời 4 quả cầu. Tính xác suất để 4 quả cầu lấy ra cùng màu.
A. \(\dfrac{{18}}{{105}}\)
B. \(\dfrac{4}{{53}}\)
C. \(\dfrac{8}{{105}}\)
D. \(\dfrac{{24}}{{105}}\)
Câu 17. Gia đình ông A xây một bể nước dạng hình hộp chữ nhật có nắp dung tích 2018 lít, đáy bể là một hình chữ nhật có chiều dài gấp ba lần chiều rộng được làm bằng bê tông có giá 250.000 đồng/m2, thân bể xây bằng gạch có giá 200.000 đồng/m2 và nắp bể được làm bằng tôn có giá 100.000 đồng/m2. Hỏi chi phí thấp nhất gia đình ông An cần bỏ ra để xây bể là bao nhiêu ? (làm tròn đến hàng đơn vị).
A. 2.017. 334 đồng
B. 2.017.333 đồng
C. 2.017.331 đồng
D. 2.017.332 đồng
Câu 18. Số nghiệm thực của phương trình \(\dfrac{{{x^2} + 5x - 8}}{{\ln \left( {x - 1} \right)}} = 0\) là :
A. 2 B. 0
C. 3 D. 1
Câu 19. Giá trị cực tiểu của hàm số \(y = {x^2}\ln x\) là :
A. \({y_{CT}} = \dfrac{1}{e}\)
B. \({y_{CT}} = - \dfrac{1}{{2e}}\)
C. \({y_{CT}} = \dfrac{1}{{2e}}\)
D. \(y = - \dfrac{1}{e}\)
Câu 20. Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, \(\widehat {ABC} = {30^0}\). Điểm M là trung điểm của cạnh AB, tam giác MA’C đều cạnh \(2a\sqrt 3 \) và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối lăng trụ ABC.A’B’C’ là :
A. \(\dfrac{{72\sqrt 2 {a^3}}}{7}\)
B. \(\dfrac{{72\sqrt 3 {a^3}}}{7}\)
C. \(\dfrac{{24\sqrt 3 {a^3}}}{7}\)
D. \(\dfrac{{24\sqrt 2 {a^3}}}{7}\)
Câu 21: Rút gọn biểu thức \(P = \sqrt {a.\sqrt[3]{{{a^2}.\sqrt[4]{{\dfrac{1}{a}}}}}} :\sqrt[{24}]{{{a^7}}},\;\;\left( {a > 0} \right)\) ta được biểu thức dạng \({a^{\dfrac{m}{n}}},\) trong đó \(\dfrac{m}{n}\) là phân số tối giản, \(m,\;\;n \in {N^*}.\) Tính giá trị \({m^2} + {n^2}.\)
A. 10 B. 25
C. 5 D. 13
Câu 22: Số các giá trị nguyên của tham số m thuộc \(\left[ { - 2018;\;2018} \right]\) để phương trình \({x^2} + \left( {m + 2} \right)x + 4 = \left( {m - 1} \right)\sqrt {{x^3} + 4x} \) có nghiệm là:
A. 2011 B. 2010
C. 2014 D. 2012
Câu 23: Biết \(\dfrac{a}{b}\) (trong đó \(\dfrac{a}{b}\) là phân số tối giản và \(a,\;b \in {N^*}\)) là giá trị của tham số m để hàm số \(y = \dfrac{2}{3}{x^3} - m{x^2} - 2\left( {3{m^2} - 1} \right)x + \dfrac{2}{3}\) có hai điểm cực trị \({x_1},\;{x_2}\) sao cho \({x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) = 1\). Tính giá trị biểu thức \(S = {a^2} + {b^2}.\)
A.\(S = 34\) B.\(S = 13\)
C.\(S = 25\) D.\(S = 10\)
Câu 24: Cho hàm số \(y = \dfrac{{2x + 2017}}{{\left| x \right| + 1}}.\) Mệnh đề nào là đúng?
A. Đồ thị hàm số có đúng một tiệm cận ngang là đường thẳng \(y = 2\) và không có tiệm có đứng.
B. Đồ thị hàm số không có tiệm cận ngang và có đúng một tiệm cận đứng là đường thẳng \(x = - 1.\)
C. Đồ thị hàm số không có tiệm cận ngang và có đúng hai tiệm cận đứng là các đường thẳng \(x = - 1;\;\;x = 1.\)
D. Đồ thị hàm số có hai tiệm cận ngang là các đường thẳng \(y = - 2;\;\;y = 2\) và không có tiệm cận đứng.
Câu 25.: Một hình lăng trụ có 2018 mặt. Hỏi hình lăng trụ đó có tất cả bao nhiêu cạnh?
A. 6045 B. 6057
C. 6048 D. 6051
Câu 26: Bất phương trình \({\left( {\dfrac{1}{2}} \right)^{{x^2} + 4x}} > \dfrac{1}{{32}}\) có tập nghiệm là \(S = \left( {a;b} \right)\). Khi đó giá trị của \(b - a\) là:
A. 2 B. 8
C. 4 D. 6
Câu 27: Có bao nhiêu giá trị nguyên dương của m để hàm số \(y = {7^{{x^3} + 3{x^2} + \left( {9 - 3m} \right)x + 1}}\) đồng biến trên \(\left[ {0;\;1} \right]?\)
A. 5 B. 3
C. Vô số D. 6
Câu 28: Tìm tập xác định D của hàm số \(y = {\log _{2017}}{\left( {x - 2} \right)^4} + {\log _{2018}}\left( {9 - {x^2}} \right).\)
A.\(D = \left[ { - 3;\;3} \right]\)
B.\(D = \left( {2;\;3} \right)\)
C.\(D = \left( { - 3;\;2} \right)\)
D. \(D = \left( { - 3;\;3} \right)\backslash \left\{ 2 \right\}\)
Câu 29: Với hai số thực dương a, b tùy ý và \(\dfrac{{{{\log }_2}a.{{\log }_5}2}}{{1 + {{\log }_5}2}} + \log b = 1.\) Khẳng định nào dưới đây là đúng?
A.\(ab = 10\)
B.\(a = 1 - b{\log _2}5\)
C.\(4a - 3b = 1\)
D.\(a{\log _2}5 + b = 1\)
Câu 30: Trong các hàm số sau, hàm số nào đồng biến trên R?
A.\(y = {\log _5}\left( {\dfrac{1}{{{x^3}}}} \right)\)
B.\(y = {\log _3}x\)
C.\(y = {2018^{\sqrt x }}\)
D.\(y = - {\left( {\dfrac{1}{2}} \right)^{{x^2} + x}}\)
Câu 31.Có bao nhiêu cặp số thực \(\left( {x;\;y} \right)\) thỏa mãn đồng thời các điều kiện \({3^{\left| {{x^2} - 2x - 3} \right| - {{\log }_3}5}} = {5^{ - \left( {y + 4} \right)}}\) và \(4\left| y \right| - \left| {y - 1} \right| + {\left( {y + 3} \right)^2} \le 8?\)
A. 4 B. 2
C. 3 D. 1
Câu 32: Tính đạo hàm của hàm số \(y = {\log _2}\left( {{x^2} + 1} \right).\)
A.\(y' = \dfrac{{2x}}{{\left( {{x^2} + 1} \right)\ln 2}}\)
B.\(y' = \dfrac{1}{{\left( {{x^2} + 1} \right)\ln 2}}\)
C.\(y' = \dfrac{{2x\ln 2}}{{\left( {{x^2} + 1} \right)}}\)
D.\(y' = \dfrac{{2x}}{{\left( {{x^2} + 1} \right)}}\)
Câu 33: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = 3\sin x + 4\cos x - 1.\)
A. \(Max\;y = 8;\;Min\;y = - 6\)
B. \(Max\;y = 4;\;Min\;y = - 6\)
C.\(Max\;y = 6;\;Min\;y = - 8\)
D. \(Max\;y = 6;\;Min\;y = - 4\)
Câu 34: Tính tổng diện tích tất cả các mặt của khối đa diện loại \(\left\{ {3;\;5} \right\}\) có cạnh bằng 1.
A.\(\dfrac{{5\sqrt 3 }}{2}\)
B.\(\dfrac{{3\sqrt 3 }}{2}\)
C.\(5\sqrt 3 \)
D.\(3\sqrt 3 \)
Câu 35: Cho phương trình \(2{\log _4}\left( {2{x^2} - x + 2m - 4{m^2}} \right)\)\(\, + {\log _{\dfrac{1}{2}}}\left( {{x^2} + mx - 2{m^2}} \right) = 0.\) Biết \(S = \left( {a;\;b} \right) \cup \left( {c;\;d} \right),\;a < b < c < d\) là tập hợp các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt \({x_1},\;{x_2}\) thỏa mãn \(x_1^2 + x_2^2 > 1.\) Tính giá trị biểu thức \(A = a + b + 5c + 2d.\)
A.\(A = 2\)
B.\(A = 1\)
C.\(A = 3\)
D.\(A = 0\)
Câu 36: Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số \(y = {x^3} - 3{x^2} + 1\) là:
A. \(y = - 2x + 1\)
B.\(y = - 2x - 1\)
C.\(y = 2x + 1\)
D.\(y = 2x - 1\)
Câu 37: Biết đường thẳng \(y = \left( {3m - 1} \right)x + 6m + 3\) cắt đồ thị hàm số \(y = {x^3} - 3{x^2} + 1\) tại 3 điểm phân biệt sao cho một giao điểm cách đều hai giao điểm còn lại. Khi đó m thuộc khoảng nào dưới đây?
A.\(\left( { - 1;\;0} \right)\)
B.\(\left( {\dfrac{3}{2};\;2} \right)\)
C.\(\left( {0;\;1} \right)\)
D.\(\left( {1;\;\dfrac{3}{2}} \right)\)
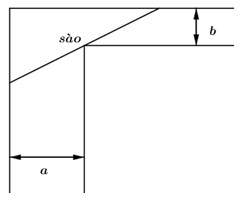
Câu 38: Để chặn đường hành lang hình chữ L, người ta dùng một que sào thẳng dài đặt kín những điểm chạm với hành lang (như hình vẽ). Biết rằng \(a = 24\) và \(b = 3\), hỏi cái sào thỏa mãn điều kiện trên có chiều dài tối thiểu là bao nhiêu?
A. \(12\sqrt 5 \)
B.\(18\sqrt 5 \)
C.\(15\sqrt 5 \)
D.\(27\sqrt 5 \)
Câu 39: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng \({60^0}\). Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC.
A. \(\dfrac{{a\sqrt 5 }}{5}\)
B.\(\dfrac{{2a\sqrt {15} }}{3}\)
C. \(\dfrac{{2a\sqrt 5 }}{5}\)
D.\(\dfrac{{5a\sqrt 3 }}{3}\)
Câu 40: Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{{e^{ax}} - {e^{3x}}}}{{2x}}\;\;\;khi\;\;x \ne 0\\\dfrac{1}{2}\;\;\;\;khi\;\;\;x = 0\end{array} \right..\) Tìm giá trị của a để hàm số \(f\left( x \right)\) liên tục tại \({x_0} = 0\).
A.\(a = 2\)
B.\(a = - \dfrac{1}{4}\)
C.\(a = 4\)
D.\(a = - \dfrac{1}{2}\)
Câu 41: Tập nghiệm của bất phương trình \({\log _2}x \le {\log _x}2\) là:
A. \(\left[ {\dfrac{1}{2};\;1} \right] \cup \left( {2; + \infty } \right)\)
B.\(\left( {0;\;\dfrac{1}{2}} \right] \cup \left( {1;\;2} \right]\)
C.\(\left( {0;\;1} \right) \cup \left( {1;\;2} \right]\)
D.\(\left[ {\dfrac{1}{2};\;2} \right]\)
Câu 42: Cho hình chóp SABCD có đáy ABCD là hình bình hành. Hai điểm M, N lần lượt thuộc các đoạn thẳng AB và AD (M và N không trùng với A) sao cho \(\dfrac{{AB}}{{AM}} + 2\dfrac{{AD}}{{AN}} = 4.\) Kí hiệu \(V,\;{V_1}\) lần lượt là thể tích của các khối chóp SABCD và SMBCDN. Tìm giá trị lớn nhất của tỉ số \(\dfrac{{{V_1}}}{V}.\)
A.\(\dfrac{2}{3}\) B. \(\dfrac{1}{6}\)
C.\(\dfrac{3}{4}\) D.\(\dfrac{{17}}{{14}}\)
Câu 43: Cho hình chóp SABC có độ dài các cạnh \(SA = BC = x;\;\;SB = AC = y;\)\(\;\;SC = AB = z\) thỏa mãn \({x^2} + {y^2} + {z^2} = 9\). Tính giá trị lớn nhất của thể tích khối chóp SABC.
A.\(\dfrac{{3\sqrt 6 }}{4}\)
B.\(\dfrac{{3\sqrt 6 }}{8}\)
C.\(\dfrac{{2\sqrt 6 }}{5}\)
D.\(\dfrac{{\sqrt 6 }}{4}\)
Câu 44: Cho x, y là các số thực dương thỏa mãn \({\log _{25}}\dfrac{x}{2} = {\log _{15}}y = {\log _9}\dfrac{{x + y}}{4}\) và \(\dfrac{x}{y} = \dfrac{{ - a + \sqrt b }}{2}\) với a, b là các số nguyên dương. Tính \(a + b\).
A.\(a + b = 3\)
B.\(a + b = 21\)
C.\(a + b = 32\)
D.\(a + b = 34\)
Câu 45: Số đường tiệm cận của đồ thị hàm số \(y = \dfrac{{\sqrt {4 - {x^2}} }}{{{x^2} - 5x + 6}}\) là:
A. 3 B. 2
C. 1 D. 0
Câu 46: Cho hai hàm số \(f\left( x \right) = {\log _{0,5}}x\) và \(g\left( x \right) = {2^{ - x}}\). Xét các mệnh đề sau:
(I) Đồ thị hàm số đối xứng nhau qua đường thẳng \(y = - x.\)
(II) Tập xác định của hai hàm số trên là R.
(III) Đồ thị của hai hàm số cắt nhau tại đúng một điểm.
(IV) Hai hàm số đều nghịch biến trên tập xác định của nó.
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 2 B. 3
C. 1 D. 4
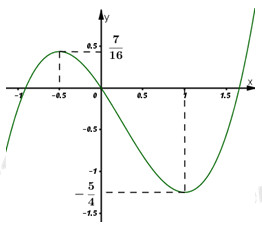
Câu 47: Cho hàm số \(y = {x^3} - \dfrac{3}{4}{x^2} - \dfrac{3}{2}x\) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của m sao cho phương trình \(4\left| {{x^3}} \right| - 3{x^2} - 6\left| x \right| = {m^2} - 6m\) có đúng ba nghiệm phân biệt.
A.\(0 < m < 3\)
B.\(m = 0\) hoặc \(m = 6\)
C. \(m > 0\) hoặc \(m < 6\)
D.\(1 < m < 6\)
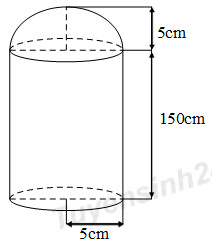
Câu 48: Một bình để chứa Oxy sử dụng trong công nghiệp và trong y tế gồm hình trụ và nửa hình cầu với thông số như hình vẽ. Thể tích V của bình này là bao nhiêu?
A.\(V = \dfrac{{26}}{3}\pi \left( {lit} \right)\)
B.\(V = \dfrac{{26}}{3}\pi \;\left( {{m^3}} \right)\)
C.\(V = \dfrac{{23}}{6}\pi \left( {lit} \right)\)
D.\(V = \dfrac{{23}}{3}\pi \left( {{m^3}} \right)\)
Câu 49: Cho hình thang cân ABCD có các cạnh đáy \(AB = 2a;\;\;CD = 4a\) và các cạnh bên \(AD = BC = 3a.\) Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD xung quanh trục đối xứng của nó.
A.\(V = \dfrac{{14\sqrt 2 }}{3}\pi {a^3}\)
B.\(V = \dfrac{4}{3}\pi {a^3}\)
C.\(V = \dfrac{{10\sqrt 2 }}{3}\pi {a^3}\)
D.\(V = \dfrac{{4 + 10\sqrt 2 }}{3}\pi {a^3}\)
Câu 50: Hàm số \(y = \dfrac{1}{3}{x^3} - 2{x^2} + 3x + 1\) đồng biến trên khoảng nào sau đây?
A.\(\left( { - \infty ;\;0} \right)\)
B.\(\left( {1;\;3} \right)\)
C.\(\left( {2; + \infty } \right)\)
D.\(\left( {0;\;3} \right)\)
Lời giải chi tiết
| 1D | 2C | 3C | 4D | 5C |
| 6B | 7B | 8D | 9C | 10D |
| 11A | 12D | 13B | 14A | 15A |
| 16C | 17D | 18D | 19B | 20B |
| 21C | 22D | 23B | 24D | 25C |
| 26D | 27B | 28D | 29A | 30D |
| 31B | 32A | 33B | 34C | 35B |
| 36B | 37A | 38C | 39A | 40C |
| 41B | 42C | 43D | 44D | 45C |
| 46A | 47B | 48C | 49A | 50A |
Xem thêm: Lời giải chi tiết Đề thi thử THPT Quốc gia môn Toán tại Tuyensinh247.com
