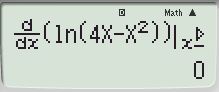Đề bài
Cho hàm số \(f\left( x \right){\rm{ }} = {\rm{ }}\ln{\rm{ }}(4x{\rm{ }}-{\rm{ }}{x^2})\). Chọn khẳng định đúng trong các khẳng định sau đây:
(A) \(f’ (2) = 1\)
(B) \(f’(2) = 0\)
(C) \(f’(5) = 1,2\)
(D) \(f’(-1) = -1,2\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Cách 1:
Sử dụng máy tính casio.
Cách 2:
Sử dụng công thức tính đạo hàm của hàm hợp: \(\left( {\ln u} \right)' = \dfrac{{u'}}{u}\).
Thay \(x = 2\) tính \(f'\left( 2 \right)\).
Lời giải chi tiết
Cách 1:
ĐK: \(4x - {x^2} > 0 \Leftrightarrow 0 < x < 4\).
Vì hàm số không xác định tại \(x = 5, x = -1\) nên (C) và (D) sai.
Sử dụng máy tính cầm tay tính \(f’(2)\) (nhập hàm và cho \(x = 2\) ấn \(=\) ta được:
Vậy chọn (B).
Cách 2:
\(\begin{array}{l}
f'\left( x \right) = \dfrac{{\left( {4x - {x^2}} \right)'}}{{4x - {x^2}}} = \dfrac{{4 - 2x}}{{4x - {x^2}}}\\
\Rightarrow f'\left( 2 \right) = \dfrac{{4 - 2.2}}{{4.2 - {2^2}}} = 0
\end{array}\)
Vậy chọn (B).