Phần 1
NGUYÊN HÀM - TÍCH PHÂN - ỨNG DỤNG
1. Nguyên hàm
a) Khái niệm
Nếu \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) trên \(K\) thì họ nguyên hàm của \(f\left( x \right)\) trên \(K\) là:
\(\int {f(x)} dx = F(x) + C,C \in R.\)
b) Tính chất
+)\(\int {f'(x)} dx = f(x) + C\)
+)\(\int {\left[ {f(x) \pm g(x)} \right]} dx\)\( = \int {f(x)} dx \pm \int {g(x)} dx\)
+)\(\int {kf(x)} dx = k\int {f(x)} dx (k \ne 0)\)
c) Nguyên hàm của một số hàm số thường gặp

d) Các phương pháp tìm nguyên hàm
- Sử dụng bảng nguyên hàm cơ bản
- Sử dụng phương pháp đổi biến số
\(\int {f\left[ {u(x)} \right].u'(x)} dx = F\left[ {u(x)} \right] + C\)
- Sử dụng phương pháp ừng phần để tìm nguyên hàm
\(\int u dv = uv - \int v du\)
2. Tích phân
a) Định nghĩa
Cho hàm số \(f\left( x \right)\) liên tục trên khoảng \(I\) và \(a,b\) là hai số bất kì thuộc \(I.\) Nếu \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) thì hiệu số \(F\left( b \right) - F\left( a \right)\) được gọi là tích phân của \(f\left( x \right)\) từ \(a\) đến \(b\) và kí hiệu là \(\int\limits_a^b {f(x)dx} .\)
Ta có công thức Newton – Leibnitz:
\(\int\limits_a^b {f(x)dx} = \left. {F\left( x \right)} \right|_a^b = F\left( b \right) - F\left( a \right)\)
b) Tính chất
+) \(\int\limits_a^a {f(x)dx} = 0\)
+) \(\int\limits_a^b {f(x)dx} = - \int\limits_b^a {f(x)dx} \)
+) \(\int\limits_a^c {f(x)dx} = \int\limits_a^b {f(x)dx} + \int\limits_b^c {f(x)dx} \)
+) \(\int\limits_a^b {kf(x)dx} = k\int\limits_a^b {f(x)dx} ,k \in R\)
+)\(\int\limits_a^b {[f(x) \pm g(x)]dx} \)\(= \int\limits_a^b {f(x)dx} \pm \int\limits_a^b {g(x)dx} \)
c) Phương pháp tính tích phân
- Sử dụng công thức Newton – Leibnitz kết hợp với bảng nguyên hàm cơ bản ở trên
- Phương pháp đổi biến số
\(\int\limits_a^b {f\left[ {u(x)} \right].u'(x)} dx = \int\limits_{u(a)}^{u(b)} {f(u)} du\)
- Phương pháp từng phần để tính tích phân
\(\int\limits_a^b u dv = \left. {uv} \right|_a^b - \int\limits_a^b v du\)
3. Ứng dụng của tích phân
a) Tính diện tích hình phẳng
+) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\) (\(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\)), trục \(Ox\) và hai đường thẳng \(x = a\) và \(x = b\) được cho bởi công thức:
\(S = \int\limits_a^b {\left| {f(x)} \right|dx} \)
+) Diện tích hình phẳng giới hạn bởi hai đường thẳng \(x = a,x = b\) và đồ thị của hai hàm số \(y = {f_1}\left( x \right)\) và \(y = {f_2}\left( x \right)\) (\({f_1}\left( x \right)\) và \({f_2}\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\)) được cho bởi công thức
\(S = \int\limits_a^b {\left| {{f_1}(x) - {f_2}(x)} \right|dx} \)
c) Tính thể tích vật thể, khối tròn xoay
+) Thể tích vật thể \(T\) có thiết diện \(S\left( x \right)\) được cho bởi công thức:
\(V = \int\limits_a^b {S(x)dx} \)
+) Cho hàm số \(y = f\left( x \right)\) liên tục và không âm trên đoạn \(\left[ {a;b} \right].\) Thể tích của vật thể tròn xoay sinh bởi miền \(\left( D \right)\) giới hạn bởi \(y = f\left( x \right),\;x = a,x = b,y = 0\) quay quanh trục \(Ox\) được cho bởi công thức:
\(V = \pi \int\limits_a^b {{y^2}dx} = \pi \int\limits_a^b {{f^2}(x)dx} \)
+) Cho hàm số \(x = f\left( y \right)\) liên tục và không âm trên đoạn \(\left[ {a;b} \right].\) Tính thể tích vật thể tròn xoay sinh bởi miền \(\left( D \right)\) giới hạn bởi \(x = f\left( y \right),\;y = a,y = b,x = 0\) quay quanh trục \(Oy\) được cho bởi công thức:
\(V = \pi \int\limits_a^b {{x^2}dy} = \pi \int\limits_a^b {{f^2}(y)dy} \)
Phần 2
SỐ PHỨC
1. Một số phức là một biểu thức có dạng a + bi, trong đó a, b là các số thực và số i thoả mãn i2 = -1. Ký hiệu số phức đó là z và viết z = a + bi.
i được gọi là đơn vị ảo
a được gọi là phần thực. Ký hiệu Re(z) = a
b được gọi là phần ảo của số phức z = a + bi, ký hiệu Im(z) = b
Tập hợp các số phức ký hiệu là C.
*) Một số lưu ý:
- Mỗi số thực a dương đều được xem như là số phức với phần ảo b = 0.
- Số phức z = a + bi có a = 0 được gọi là số thuần ảo hay là số ảo.
- Số 0 vừa là số thực vừa là số ảo.
2. Hai số phức bằng nhau.
Cho z = a + bi và z’ = a’ + b’i.
\[z = z' \Leftrightarrow \left\{ \begin{array}{l}
a = a'\\
b = b'
\end{array} \right.\]
3. Biểu diễn hình học của số phức.
Mỗi số phức được biểu diễn bởi một điểm M(a;b) trên mặt phẳng toạ độ Oxy.
Ngược lại, mỗi điểm M(a;b) biểu diễn một số phức là z = a + bi.
4. Phép cộng và phép trừ các số phức.
Cho hai số phức z = a + bi và z’ = a’ + b’i. Ta định nghĩa:
\(\left\{ \begin{array}{l}z + z' = (a + a') + (b + b')i\\z - z' = (a - a') + (b - b')i\end{array} \right.\)
5. Phép nhân số phức.
Cho hai số phức z = a + bi và z’ = a’ + b’i. Ta định nghĩa:
\(zz' = aa' - bb' + (ab' + a'b)i\)
6. Số phức liên hợp.
Cho số phức z = a + bi. Số phức \(\overline z \) = a – bi gọi là số phức liên hợp với số phức trên.
Vậy \(\overline z \) = \(\overline {a + bi} \)= a - bi
Chú ý:
10) \(\overline {\overline z } \) = z (z và \(\overline z \) gọi là hai số phức liên hợp với nhau.
20) z.\(\overline z \) = a2 + b2
*) Tính chất của số phức liên hợp:
(1): \(\overline{\overline z} = z\)
(2): \(\overline {z + z'} = \overline z + \overline {z'} \)
(3): \(\overline {z.z'} = \overline z .\overline {z'} \)
(4): z.\(\overline z \)= \(\sqrt {{a^2} + {b^2}} \)(z = a + bi)
7. Môđun của số phức.
Cho số phức z = a + bi. Ta ký hiệu \(\left| z \right|\) là môđun của số phư z, đó là số thực không âm được xác định như sau:
- Nếu M(a;b) biểu diễn số phc z = a + bi, thì \(\left| z \right|\) = =\(\sqrt {{a^2} + {b^2}} \)
- Nếu z = a + bi, thì \(\left| z \right|\) = \(\sqrt {z.\overline z } \)=\(\sqrt {{a^2} + {b^2}} \)
8. Phép chia số phức khác 0.
Cho số phức z = a + bi ≠ 0 (tức là a2+b2 > 0)
Ta định nghĩa số nghịch đảo z-1 của số phức z ≠ 0 là số
z-1= \(\frac{1}{{{a^2} + {b^2}}}\overline z = \frac{1}{{{{\left| z \right|}^2}}}\overline z \)
Thương \(\frac{{z'}}{z}\)của phép chia số phức z’ cho số phức z ≠ 0 được xác định như sau:
\(\frac{{z'}}{z} = z'.{z^{ - 1}} = \frac{{z'.\overline z }}{{{{\left| z \right|}^2}}}\)
Với các phép tính cộng, trừ, nhân chia số phức nói trên nó cũng có đầy đủ tính chất giao hoán, phân phối, kết hợp như các phép cộng, trừ, nhân, chia số thực thông thường.
Phần 3
PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
1. Hệ trục tọa độ trong không gian
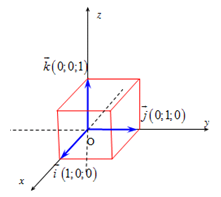
+) \({\overrightarrow i ^2} = {\overrightarrow j ^2} = {\overrightarrow k ^2} = 1\)
\(\overrightarrow i .\overrightarrow j = \overrightarrow i .\overrightarrow k \,\, = \,\,\overrightarrow k .\overrightarrow j = 0\)
+) \(\vec 0 = (0;0;0),\,\,\vec i = (1;0;0),\) \(\vec j = (0;1;0),\,\,\vec k = (0;0;1)\)
2. Các công thức điểm, véc tơ
+) \(\vec a \pm \vec b\, = \,\,({a_1} \pm {b_1};\,\,{a_2} \pm {b_2};\,\,{a_3} \pm {b_3})\)
+) \(k\vec a\,\, = \,\,(k{a_1};\,\,k{a_2};\,\,k{a_3})\)
+) \(\overrightarrow a = \overrightarrow b \,\, \Leftrightarrow \,\,\left\{ \begin{array}{l}{a_1} = {b_1}\\{a_2} = {b_2}\\{a_3} = {b_3}\end{array} \right.\)
+) \(\overrightarrow a \) cùng phương \(\overrightarrow b \,(\vec b \ne \vec 0)\,\) \( \Leftrightarrow \overrightarrow a = k\overrightarrow b \,\,\,(k \in \mathbb{R})\)
\( \Leftrightarrow \,\,\left\{ \begin{array}{l}{a_1} = k{b_1}\\{a_2} = k{b_2}\\{a_3} = k{b_3}\end{array} \right. \Leftrightarrow \,\,\frac{{{a_1}}}{{{b_1}}} = \frac{{{a_2}}}{{{b_2}}} = \frac{{{a_3}}}{{{b_3}}},\)\(({b_1},\,\,{b_2},\,\,{b_3} \ne 0)\)
+) \(\vec a.\vec b = {a_1}.{b_1} + {a_2}.{b_2} + {a_3}.{b_3}\)
+) \(\overrightarrow a \bot \overrightarrow b \,\,\, \Leftrightarrow \,\,\,{a_1}{b_1} + {a_2}{b_2} + {a_3}{b_3} = 0\)
+) \({\vec a^2} = a_1^2 + a_2^2 + a_3^2\)
+) \(\left| {\vec a} \right| = \,\,\sqrt {a_1^2 + a_2^2 + a_2^2} \)
+) \(\cos (\vec a,\,\,\vec b)\,\, = \,\frac{{\vec a.\vec b}}{{\left| {\vec a} \right|.\left| {\vec b} \right|}}\,\)\(\, = \,\,\frac{{{a_1}{b_1} + {a_2}{b_2} + {a_3}{b_3}}}{{\sqrt {a_1^2 + a_2^2 + a_3^2} .\sqrt {b_1^2 + b_2^2 + b_3^2} }}\) (với \(\vec a,\,\,\vec b \ne \vec 0\))
+) \(\begin{array}{l}M \in \left( {Oxy} \right) \Leftrightarrow z = 0\\M \in \left( {Oyz} \right) \Leftrightarrow x = 0\\M \in \left( {Oxz} \right) \Leftrightarrow y = 0\end{array}\)
+)\(\begin{array}{l}M \in Ox \Leftrightarrow y = z = 0;\\M \in Oy \Leftrightarrow x = z = 0;\\M \in Oz \Leftrightarrow x = y = 0\end{array}\)
+) \(\overrightarrow {AB} \)\(= ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A})\)
+) \(AB\)\(= \,\,\sqrt {{{({x_B} - {x_A})}^2} + {{({y_B} - {y_A})}^2} + {{({z_B} - {z_A})}^2}} \)
+) Toạ độ trung điểm \(M\) của đoạn thẳng \(AB\): \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2}} \right)\)
+) Toạ độ trọng tâm \(G\) của tam giác \(ABC\):
\(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3}} \right)\)
+) Toạ độ trọng tâm \(G\) của tứ diện \(ABCD\):
\(G\left( {\frac{{{x_A} + {x_B} + {x_C} + {x_D}}}{4};\frac{{{y_A} + {y_B} + {y_C} + {y_D}}}{4};\frac{{{z_A} + {z_B} + {z_C} + {z_D}}}{4}} \right)\)
+) \(\begin{array}{l}\left[ {\vec a,\vec b} \right]\\ = \,\,\left( {\left| {\begin{array}{*{20}{c}}{{a_2}}&{{a_3}}\\{{b_2}}&{{b_3}}\end{array}} \right|\,\,;\,\,\left| {\begin{array}{*{20}{c}}{{a_3}}&{{a_1}}\\{{b_3}}&{{b_1}}\end{array}} \right|\,\,;\,\,\left| {\begin{array}{*{20}{c}}{{a_1}}&{{a_2}}\\{{b_1}}&{{b_2}}\end{array}} \right|} \right)\\ = \left( {{a_2}{b_3} - {a_3}{b_2};{a_3}{b_1} - {a_1}{b_3};{a_1}{b_2} - {a_2}{b_1}} \right)\end{array}\)
+) \([\overrightarrow a ,\,\,\overrightarrow b ]\,\, \bot \,\,\overrightarrow a ;[\overrightarrow a ,\,\,\overrightarrow b ]\,\, \bot \,\,\overrightarrow b \)
+) \(\left[ {\overrightarrow a ,\,\,\overrightarrow b \,} \right] = - \left[ {\overrightarrow b ,\overrightarrow a } \right]\)
+) \(\left[ {\vec i,\vec j} \right] = \vec k;\left[ {\vec j,\vec k} \right] = \vec i;\left[ {\vec k,\vec i} \right] = \vec j\)
+) \(\overrightarrow a ,\,\,\overrightarrow b \) cùng phương \( \Leftrightarrow [\overrightarrow a ,\,\,\overrightarrow b ]\,\, = \,\,\overrightarrow 0 \) (chứng minh \(3\) điểm thẳng hàng)
+) \(\vec a,\vec b,\vec c\) đồng phẳng \( \Leftrightarrow \left[ {\vec a,\vec b} \right].\vec c = 0\)
+) Diện tích hình bình hành \(ABCD\):
\({S_{ABCD}} = \left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AD} } \right]} \right|\)
+) Diện tích tam giác \(ABC\):
\({S_{\Delta ABC}} = \frac{1}{2}\left| {\left[ {\overrightarrow {AB} ,\,\,\overrightarrow {AC} } \right]} \right|\)
+) Thể tích khối hộp \(ABCD.A'B'C'D'\):
\({V_{ABCD.A'B'C'D'}}\,\, = \,\,\left| {[\overrightarrow {AB} ,\,\,\overrightarrow {AD} ].\overrightarrow {AA'} } \right|\)
+) Thể tích tứ diện \(ABCD\):
\({V_{ABCD}} = \frac{1}{6}\left| {[\overrightarrow {AB} ,\,\,\overrightarrow {AC} ]\,.\overrightarrow {AD} } \right|\)
2. Phương trình mặt phẳng
+) Trong không gian \(Oxyz\), mọi mặt phẳng đều có dạng phương trình:
\(Ax + By + Cz + D = 0\,\,\) với \({A^2} + {B^2} + {C^2} \ne 0\)
+) Nếu mặt phẳng \((\alpha )\) có phương trình \(Ax + By + Cz + D = 0\,\,\)thì nó có một VTPT là \(\overrightarrow n (A;\,B;\,C)\).
+) Phương trình mặt phẳng đi qua điểm \({M_0}({x_0};{y_0};{z_0})\) và nhận vectơ \(\overrightarrow n (A;\,B;\,C)\) khác \(\overrightarrow 0 \) là VTPT là: \(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\).
+) Nếu \(\overrightarrow n \) là một VTPT của mặt phẳng \((\alpha )\) thì \(k\overrightarrow n \,\)\(\,(k \ne 0)\) cũng là một VTPT của mặt phẳng\((\alpha )\)
+) Một mặt phẳng được xác định duy nhất nếu biết một điểm nó đi qua và một VTPT của nó.
+) Nếu \(\overrightarrow u ,\,\overrightarrow v \) có giá song song hoặc nằm trên mặt phẳng \((\alpha )\) thì \(\overrightarrow n = {\rm{[}}\overrightarrow u ,\,\overrightarrow v {\rm{]}}\) là một VTPT của \((\alpha )\).
+) Khoảng cách từ điểm \({M_0}\) đến mặt phẳng \((\alpha )\) được tính: \(d({M_0},(\alpha )) = \frac{{|A{x_0} + B{y_0} + C{z_0} + D|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\)
+) Góc giữa \(\left( \alpha \right)\) và \(\left( \beta \right)\) bằng hoặc bù với góc giữa hai VTPT \(\overrightarrow {{n_\alpha }} ,\overrightarrow {{n_\beta }} \). Tức là:
\(\begin{array}{l}\cos \left( {\left( \alpha \right),\left( \beta \right)} \right)\\ = \left| {\cos \left( {\overrightarrow {{n_\alpha }} ,\overrightarrow {{n_\beta }} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_\alpha }} .\overrightarrow {{n_\beta }} } \right|}}{{\left| {\overrightarrow {{n_\alpha }} } \right|.\left| {\overrightarrow {{n_\beta }} } \right|}}\\ = \frac{{\left| {{A_1}{A_2} + {B_1}{B_2} + {C_1}{C_2}} \right|}}{{\sqrt {A_1^2 + B_1^2 + C_1^2} .\sqrt {A_2^2 + B_2^2 + C_2^2} }}\end{array}\)
+) \((\alpha ){\rm{//}}(\beta )\) \(\Leftrightarrow \frac{{{A_1}}}{{{A_2}}} = \frac{{{B_1}}}{{{B_2}}} = \frac{{{C_1}}}{{{C_2}}} \ne \frac{{{D_1}}}{{{D_2}}}\)
+) \((\alpha ) \equiv (\beta )\)\(\Leftrightarrow \frac{{{A_1}}}{{{A_2}}} = \frac{{{B_1}}}{{{B_2}}} = \frac{{{C_1}}}{{{C_2}}} = \frac{{{D_1}}}{{{D_2}}}\)
+) \((\alpha )\) cắt \((\beta )\)\(\Leftrightarrow \frac{{{A_1}}}{{{A_2}}} \ne \frac{{{B_1}}}{{{B_2}}}\) hoặc \(\frac{{{B_1}}}{{{B_2}}} \ne \frac{{{C_1}}}{{{C_2}}}\) hoặc \(\frac{{{A_1}}}{{{A_2}}} \ne \frac{{{C_1}}}{{{C_2}}}\)
3. Phương trình đường thẳng
+) Phương trình tham số: \(\left\{ \begin{array}{l}x = {x_0} + {a_1}t\\y = {y_0} + {a_2}t\\z = {z_0} + {a_2}t\end{array} \right.;{\rm{ }}\left( {t \in \mathbb{R}} \right)\) với \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) là điểm đi qua và \(\overrightarrow u = \left( {{a_1};{a_2};{a_3}} \right)\) là VTCP \(\left( {{a_1}^2 + {a_2}^2 + {a_3}^2 \ne 0} \right)\)
+) Phương trình chính tắc: \(\frac{{x - {x_0}}}{{{a_1}}} = \frac{{y - {y_0}}}{{{a_2}}} = \frac{{z - {z_0}}}{{{a_3}}}\) với \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) là điểm đi qua và \(\overrightarrow u = \left( {{a_1};{a_2};{a_3}} \right)\) là VTCP \(\left( {{a_1}{a_2}{a_3} \ne 0} \right)\)
+) Gọi \(\varphi \) là góc giữa hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\). Ta có: \(\cos \varphi = \frac{{\left| {\overrightarrow {{u_1}} .\overrightarrow {{u_2}} } \right|}}{{\left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{u_2}} } \right|}}\)
+) Gọi \(\varphi \) là góc giữa đường thẳng \(\Delta \) và mặt phẳng \((\alpha )\). Ta có: \(\sin \varphi = \frac{{\left| {\overrightarrow {{u_\Delta }} .\overrightarrow {{n_\alpha }} } \right|}}{{\left| {\overrightarrow {{u_\Delta }} } \right|.\left| {\overrightarrow {{n_\alpha }} } \right|}}\)
+) Khoảng cách từ điểm \(M\) đến đường thẳng \(\Delta \) đi qua điểm \({M_0}\) và có vectơ chỉ phương \(\overrightarrow {{u_\Delta }} \)
\(d\left( {M,\Delta } \right) = \frac{{\left| {\left[ {\overrightarrow {{u_\Delta }} ,\overrightarrow {{M_0}M} } \right]} \right|}}{{\left| {\overrightarrow {{u_\Delta }} } \right|}}\)
+) Khoảng cách giữa hai đường thẳng chéo nhau:
\({\Delta _1}\) đi qua điểm \(M\) và có vectơ chỉ phương \(\overrightarrow {{u_1}} \)
\({\Delta _2}\) đi qua điểm \(N\) và có vectơ chỉ phương \(\overrightarrow {{u_2}} \)
\(d\left( {{\Delta _1},{\Delta _2}} \right){\rm{ = }}\frac{{\left| {\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right].\overrightarrow {MN} } \right|}}{{\left| {\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right]} \right|}}\)
+) Vị trí tương đối của hai đường thẳng
\(d\) song song \(d'\) \(\Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u = k\overrightarrow {u'} \\M \in d,M \notin d'\end{array} \right.\)
\(d\) trùng \(d'\) \(\Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u = k\overrightarrow {u'} \\M \in d,M \in d'\end{array} \right.\)
\(d\) cắt \(d'\) \(\Leftrightarrow \left[ {\overrightarrow u ,\overrightarrow {u'} } \right].\overrightarrow {MN} = 0\) và \(\overrightarrow u ,\overrightarrow {u'} \) không cùng phương
\(d\) chéo \(d'\) \(\Leftrightarrow \left[ {\overrightarrow u ,\overrightarrow {u'} } \right].\overrightarrow {MN} \ne 0\)
4. Phương trình mặt cầu
+) Phương trình chính tắc
Mặt cầu \(\left( S \right):\)\({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\) có tâm \(I\left( {a;b;c} \right)\), bán kính \(R > 0\)
+) Phương trình tổng quát
Mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) có tâm \(I\left( {a;b;c} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \) với \({a^2} + {b^2} + {c^2} - d > 0\)

