Đề bài
Trong tất cả các hình chữ nhật cùng có diện tích \(48 m^2\) , hãy xác định hình chữ nhật có chu vi nhỏ nhất.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Cho hình chữ nhật có chiều dài là \(x\) và chiều rộng là \(y.\)
+) Chu vi của hình chữ nhật đó là: \(P=2\left( x+y \right).\)
+) Diện tích của hình chữ nhật đó là: \(S=xy.\)
Lập hàm số \(P(x)\), xét hàm suy ra GTNN.
Lời giải chi tiết
Gọi chiều rộng và chiều dài của hình chữ nhật lần lượt là \(x;\ y\ \left( m \right),\ \ \left( x;\ y > 0 \right).\)
Theo đề bài ta có diện tích hình chữ nhật là \(48\ {{m}^{2}}\Rightarrow xy=48\Leftrightarrow y=\dfrac{48}{x}.\)
\(\Rightarrow \) Chu vi hình chữ nhật đó là: \(P=2\left( x+y \right)=2\left( x+\dfrac{48}{x} \right).\)
Xét hàm số \(P\left( x \right)=2\left( x+\dfrac{48}{x} \right)\) trên \(\left( 0;+\infty \right)\) ta có:
\(\begin{array}{l}
P'\left( x \right) = 2\left( {1 - \dfrac{{48}}{{{x^2}}}} \right)\\= 2\left( {\dfrac{{{x^2} - 48}}{{{x^2}}}} \right)\\ \Rightarrow P'\left( x \right) = 0 \Leftrightarrow {x^2} - 48 = 0\\
\Leftrightarrow {x^2} = 48 \Leftrightarrow \left[ \begin{array}{l}
x = 4\sqrt 3 \in \left( {0; + \infty } \right)\\
x = - 4\sqrt 3\notin \left( {0; + \infty } \right)
\end{array} \right..
\end{array}\)
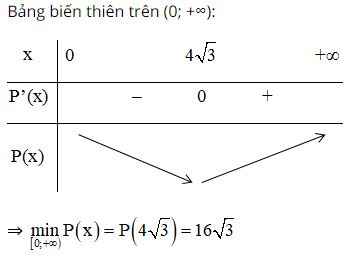
Ta có: \(P\left( 4\sqrt{3} \right)=16\sqrt{3}.\)
Vậy hình chữ nhật có chu vi nhỏ nhất là hình vuông có cạnh \(4\sqrt{3}m.\)