LG a
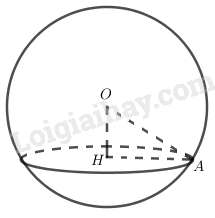
a) Hãy xác định đường tròn giao tuyến của mặt cầu S(O; r) và mặt phẳng (α) biết rằng khoảng cách từ tâm O đến (α) bằng \({r \over 2}\)
Phương pháp giải:
- Dựng hình, tính bán kính của từng đường tròn giao tuyến bằng cách áp dụng định lý Pi-ta-go.
- Từ đó kết luận cho từng câu a, b.
Lời giải chi tiết:
Xét tam giác \(OAH\) vuông tại \(H\) có \(OA = r,OH = \dfrac{r}{2}\) nên: \(HA = \sqrt {O{A^2} - O{H^2}} \) \( = \sqrt {{r^2} - \dfrac{{{r^2}}}{4}} = \dfrac{{r\sqrt 3 }}{2}\).
Vậy đường tròn giao tuyến có bán kính \(\dfrac{{r\sqrt 3 }}{2}\).
LG b
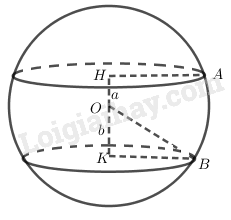
b) Cho mặt cầu S(O; r), hai mặt phẳng (α) và (β) có khoảng cách đến tâm O của mặt cầu đã cho lần lượt là a và b (0 < a < b < r). Hãy so sánh hai bán kính của các đường tròn giao tuyến.
Phương pháp giải:
- Dựng hình, tính bán kính của từng đường tròn giao tuyến bằng cách áp dụng định lý Pi-ta-go.
- Từ đó kết luận cho từng câu a, b.
Lời giải chi tiết:
Xét tam giác \(OHA\) vuông tại \(H\) có \(HA = \sqrt {O{A^2} - O{H^2}} \) \( = \sqrt {{r^2} - {a^2}} \)
Xét tam giác \(OKB\) vuông tại \(K\) có \(KB = \sqrt {O{B^2} - O{K^2}} \) \( = \sqrt {{r^2} - {b^2}} \)
Mà \(0 < a < b < r\) nên \(0 < {r^2} - {b^2} < {r^2} - {a^2}\) \( \Rightarrow \sqrt {{r^2} - {b^2}} < \sqrt {{r^2} - {a^2}} \) hay \(KB < HA\).
Vậy đường tròn cắt bởi \(\left( \beta \right)\) có bán kính nhỏ hơn bán kính đường tròn cắt bởi \(\left( \alpha \right)\).