Video hướng dẫn giải
Trong không gian \(Oxyz\), cho hai điểm \(A(1 ; 2 ;-1), B(7 ; -2 ; 3)\) và đường thẳng \(d\) có phương trình: \(\left\{ \matrix{x = - 1 + 3t \hfill \cr y = 2 - 2t \hfill \cr z = 2 + 2t. \hfill \cr} \right.\)
LG a
Chứng minh rằng hai đường thẳng \(d\) và \(AB\) cùng nằm trong một mặt phẳng.
Phương pháp giải:
Chứng minh AB // d. Suy ra AB và d cùng thuộc một mặt phẳng.
Lời giải chi tiết:
Đường thẳng \(AB\) có vectơ chỉ phương \(\overrightarrow {AB} =(6; -4; 4)\)
Đường thẳng \((d)\) có vectơ chỉ phương \(\overrightarrow a = (3; -2; 2)\)
\( \Rightarrow \) \(\overrightarrow {AB} = 2\overrightarrow a \) và \(A ∉ (d)\)
\( \Rightarrow AB\) và \((d)\) song song với nhau.
\( \Rightarrow \) Hai đường thẳng \((d)\) và \(AB\) cùng thuộc một mặt phẳng.
LG b
Tìm điểm \(I\) trên \(d\) sao cho \(AI + BI\) nhỏ nhất.
Phương pháp giải:
Gọi A' là điểm đối xứng với A qua d, khi đó ta có IA = IA' \( \Rightarrow IA + IB = IA' + IB \ge A'B\).
Dấu bằng xảy ra \( \Leftrightarrow I = d \cap A'B\).
Lời giải chi tiết:
Gọi \(A'\) là điểm đối xứng của điểm \(A\) qua phép đối xứng qua đường thẳng \(d\) thì điểm \(I\) cần tìm là giao điểm của đường thẳng \(A'B\) và đường thẳng \(d\).
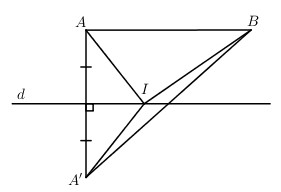
Trong câu a) ta chứng minh được \(AB // d\), từ đó suy ra \(I\) chính là giao điểm của đường thẳng \(d\) với mặt phẳng trung trực của đoạn thẳng \(AB\).
Gọi \(M\) là trung điểm của \(AB\) thì \(M(4; 0; 1)\).
Phương trình mặt phẳng trung trực của \(AB\):
\(3(x - 4) - 2(y - 0) + 2(z - 1) = 0\) \( \Rightarrow 3x - 2y + 2z - 14 = 0\)
Phương trình tham số của \((d)\):\(\left\{ \matrix{
x = - 1 + 3t \hfill \cr
y = 2 - 2t \hfill \cr
z = 2 + 2t \hfill \cr} \right.\)
Giá trị tham số ứng với giao điểm \(I \)của \((d)\) và mặt phẳng trung trực của \(AB\) là nghiệm của phương trình:
\(3( -1 + 3t) - 2(2 - 2t) + 2(2 + 2t) - 14 = 0\) \( \Rightarrow t = 1\)
Từ đây ta được \(I (2; 0; 4)\)
Cách khác:
Gọi M là trung điểm của AB, H là giao điểm của AA’ với d.
IH//AB, H là trung điểm AA’ nên I là trung điểm A’B.
Mà M là trung điểm AB nên MI là đường trung bình của tam giác AA’B.
\( \Rightarrow MI//AA'\), mà \(AA' \bot d \Rightarrow MI \bot d\).
Ta có: \(M\left( {4;0;1} \right)\), \(I\left( { - 1 + 3t;2 - 2t;2 + 2t} \right)\)
\( \Rightarrow \overrightarrow {MI} = \left( { - 5 + 3t;2 - 2t;1 + 2t} \right)\)
\(\overrightarrow {{u_d}} = \left( {3; - 2;2} \right)\)
\(MI \bot d \Rightarrow \overrightarrow {MI} .\overrightarrow {{u_d}} = 0\) \( \Leftrightarrow 3\left( { - 5 + 3t} \right) - 2\left( {2 - 2t} \right) + 2\left( {1 + 2t} \right) = 0\)
\( \Leftrightarrow - 15 + 9t - 4 + 4t + 2 + 4t = 0\)
\(\begin{array}{l} \Leftrightarrow - 17 + 17t = 0\\ \Leftrightarrow t = 1\\ \Rightarrow I\left( {2;0;4} \right)\end{array}\)

