Đề bài
Tính thể tích khối tứ diện đều cạnh \(a\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Gọi \(AH\) là đường cao hạ từ đỉnh \(A\) của tứ diện đều \(ABCD\) \(\left({H \in (BCD)} \right)\).
+) Do tứ diện \(ABCD\) đều, chứng minh \(H\) là trọng tâm tam giác \(ABC\).
+) Sử dụng định lí Pytago tính độ dài \(AH\).
+) Áp dụng công thức tính thể tích: \({V_{ABCD}} = \dfrac{1}{3}AH.{S_{BCD}}\).
Lời giải chi tiết
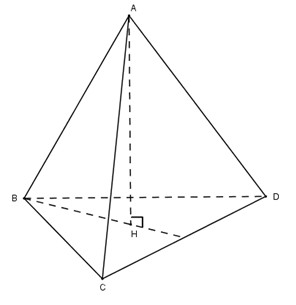
Cho tứ diện đều \(ABCD\). Hạ \(AH \bot \left( {BCD} \right)\)
Dễ dàng chứng minh được \({\Delta _v}AHB = {\Delta _v}AHC = {\Delta _v}AHD\,\,\left( {ch - cgv} \right) \) \(\Rightarrow HB = HC = HD,\) do đó H là tâm đường tròn ngoại tiếp tam giác \(BCD\).
Do \(BCD\) là tam giác đều nên \(H\) là trọng tâm của tam giác \(BCD\).
Gọi \(M\) là trung điểm \(CD\) thì \(BM\) vừa là trung tuyến vừa là đường cao trong tam giác.
Ta có: \(BM = BD\sin {60^0} = \frac{{a\sqrt 3 }}{2}\)
Do đó \(BH = \frac{2}{3}BM= \displaystyle{2 \over 3}.{{\sqrt 3 } \over 2}a = {{\sqrt 3 } \over 3}a\)
Áp dụng định lí Pitago trong tam giác vuông \(ABH\) ta có: \(A{H^2} = A{B^2} - B{H^2} = {a^2} - \dfrac{{{a^2}}}{3} = \dfrac{{2{a^2}}}{3} \) \(\Rightarrow AH = \dfrac{{a\sqrt 6 }}{3}\)
Do tam giác \(BCD\) đều cạnh \(a\) nên: \({S_{BCD}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Vậy \({V_{ABCD}} = \dfrac{1}{3}AH.{S_{BCD}} \) \(= \dfrac{1}{3}.\dfrac{{a\sqrt 6 }}{3}.\dfrac{{{a^2}\sqrt 3 }}{4} \) \(= \dfrac{{{a^3}\sqrt 2 }}{{12}}.\)

