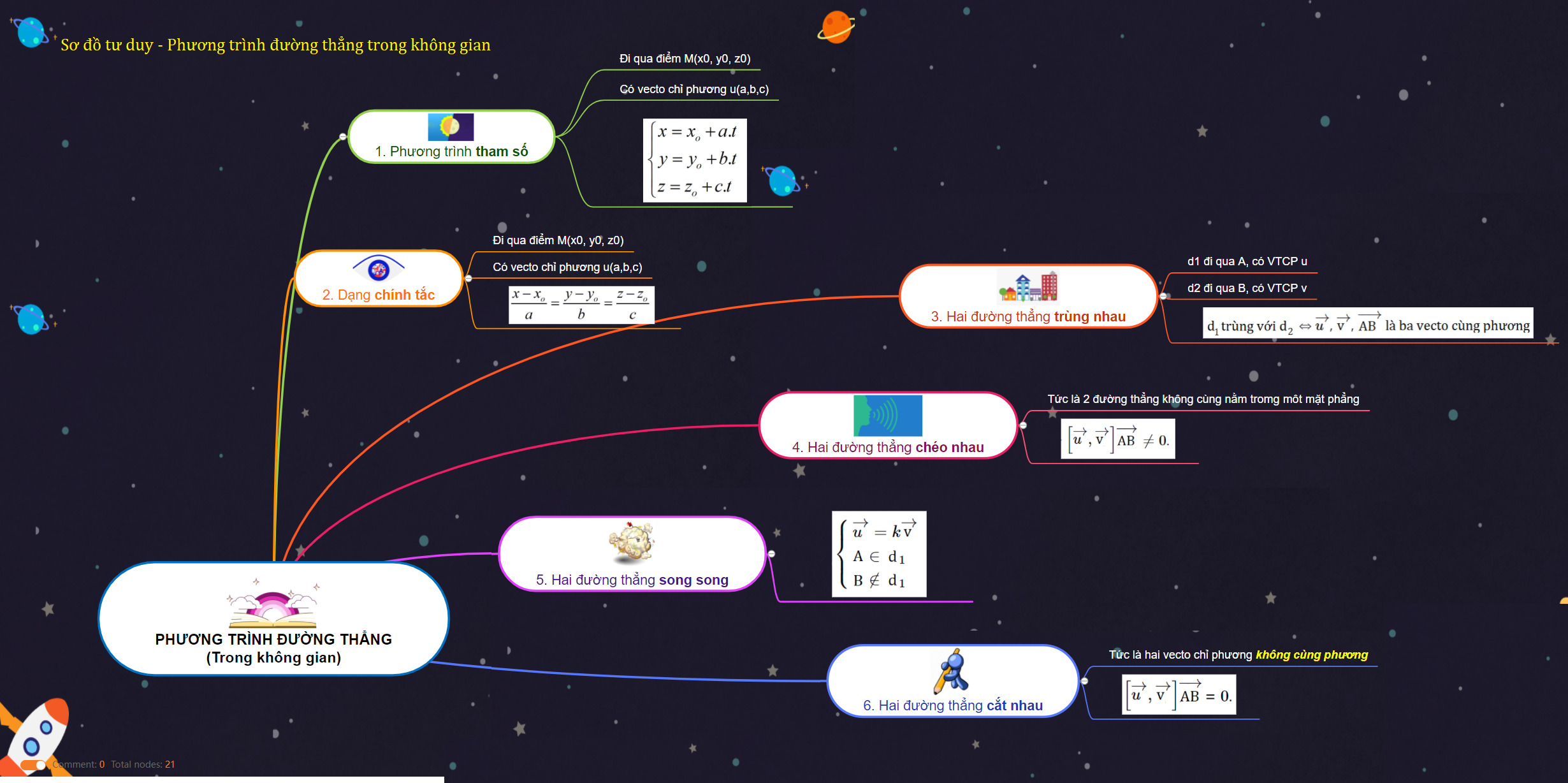
1. Phương trình tham số
Đường thẳng \(∆\) qua điểm \({M_0}({x_0};{y_0};{z_0})\) có vectơ chỉ phương \(\overrightarrow{a}\)(a1 ; a2 ; a3) có phương trình tham số dạng:
\(\left\{\begin{matrix} x=x_{0}+ a_{1}t & & \\ y= y_{0}+a_{2}t & & \\ z=z_{0}+a_{3}t & & \end{matrix}\right.\), t ∈ R là tham số.
Nếu \({a_1},\;{a_2},\;{a_3}\) đều khác không, ta viết phương trình trên ở dạng chính tắc:
\(\dfrac{x-x_{0}}{a_{1}}=\dfrac{y-y_{0}}{a_{2}}=\dfrac{z-z_{0}}{a_{3}}.\)
2. Vị trí tương đối
Cho đường thẳng \({\Delta _1}\) qua điểm \(\;{M_1}\) và có vec tơ chỉ phương \(\overrightarrow{u_{1}}\), đường thẳng \({\Delta _2}\) qua điểm \(\;{M_2}\) và có vec tơ chỉ phương \(\overrightarrow{u_{2}}\).
* \({\Delta _1}\) và \({\Delta _2}\) chéo nhau \(\Leftrightarrow \;{\Delta _1}\) và \({\Delta _2}\) không nằm trong cùng một mặt phẳng ⇔ \(\left [\overrightarrow{u_{1}},\overrightarrow{u_{2}} \right ]\overrightarrow{M_{1}M_{2}}\neq 0\).
* \({\Delta _1}\) và \({\Delta _2}\) song song ⇔ \(\left\{\begin{matrix} \overrightarrow{u_{1}}=k\overrightarrow{u_{2}}\\ M_{1}\in \Delta _{1}\\ M_{2}\notin \Delta _{1} \end{matrix}\right.\).
* \({\Delta _1}\) trùng với \({\Delta _2}\) ⇔ \(\overrightarrow{u_{1}}\), \(\overrightarrow{u_{2}}\), \(\overrightarrow{M_{1}M_{2}}\) là ba vectơ cùng phương.
* \({\Delta _1}\) cắt \({\Delta _2}\) ⇔ \(\overrightarrow{u_{1}},\overrightarrow{u_{2}}\) không cùng phương và \(\left [\overrightarrow{u_{1}},\overrightarrow{u_{2}} \right ]\overrightarrow{M_{1}M_{2}}= 0\).