Cho điểm M(1; -1; 2) và mặt phẳng (α): 2x – y + 2z + 12 = 0
LG a
Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng (α);
Phương pháp giải:
- Viết phương trình tham số của đường thẳng Δ đi qua M và vuông góc (α).
- Tìm giao điểm của Δ và (α).
Lời giải chi tiết:
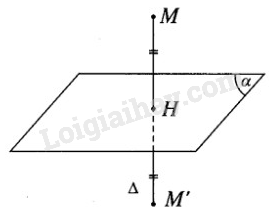
Phương trình tham số của đường thẳng Δ đi qua điểm M(1; -1; 2) và vuông góc với mặt phẳng (α) : 2x – y + 2z + 12 = 0 là: Δ:{x=1+2ty=−1−tz=2+2t
Xét điểm H(1 + 2t; -1 – t ; 2 + 2t) ∈Δ
Ta có H∈(α)⇔2(1+2t)+(1+t)+2(2+2t)+12=0 ⇔t=−199
Vậy ta được H(−299;109;−209)
LG b
Tìm tọa độ điểm M’ đối xứng với M qua mặt phẳng (α).
Phương pháp giải:
M′ đối xứng với M qua (α) ⇔H là trung điểm của MM′.
Lời giải chi tiết:
H là trung điểm của MM’, suy ra xM′=2xH−xM=−589−1=−679
yM′=2yH−yM=209+1=299
zM′=2zH−zM=−409−2=−589
Vậy ta được M′(−679;299;−589)
