Chọn đáp án đúng:
3.77
Phương trình chính tắc của đường thẳng đi qua hai điểm A(1; 2; -3) và B(3; -1; 1) là:
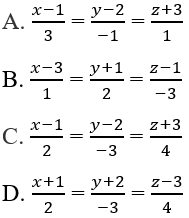
Lời giải chi tiết:
Ta có: \(\overrightarrow {AB} = \left( {2; - 3;4} \right)\)
Đường thẳng AB đi qua điểm A(1; 2; -3) và có vectơ chỉ phương là \(\overrightarrow {AB} = \left( {2; - 3;4} \right)\) nên có phương trình chính tắc là: \(\dfrac{{x - 1}}{2} = \dfrac{{y - 2}}{{ - 3}} = \dfrac{{z + 3}}{4}\)
Chọn C.
3.78
Tọa độ giao điểm M của đường thẳng \(d:\dfrac{{x - 12}}{4} = \dfrac{{y - 9}}{3} = \dfrac{{z - 1}}{1}\) và mặt phẳng (α): 3x + 5y - z - 2 = 0 là:
A. (1; 0; 1) B. (0; 0; -2)
C. (1; 1; 6) D. (12; 9; 1)
Lời giải chi tiết:
Gọi M(12 + 4t; 9 + 3t; 1 + t) thuộc d và mặt phẳng (α),
Thay tọa độ M vào phương trình (α) ta được phương trình theo t:
3(12 + 4t) + 5(9 + 3t) - (1 + t) - 2 = 0
\( \Leftrightarrow 36 + 12t + 45 + 15t - 1 - t - 2 = 0\)
\( \Leftrightarrow 26t + 78 = 0 \Leftrightarrow t = - 3\)
Vậy d cắt (α) tại M(0; 0; -2).
Chọn B.
3.79
Cho đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + t\\y = 2 - t\\z = 1 + 2t\end{array} \right.\) và mặt phẳng (α): x + 3y + z + 1 = 0
Khẳng định nào sau đây là đúng?
A. d // (α) B. d cắt (α)
C. d ⊂ (α) D. d ⊥ (α)
Lời giải chi tiết:
Đường thẳng d có vectơ chỉ phương là \(\overrightarrow u = \left( {1; - 1;2} \right)\)
Mặt phẳng (α) có vectơ pháp tuyến \(\overrightarrow n = \left( {1;3;1} \right)\)
Ta thấy: \(\overrightarrow u .\overrightarrow n = 1.1 - 1.3 + 2.1 = 0\) nên \(\overrightarrow u \bot \overrightarrow n \)
Mà điểm cố định M(1; 2; 1) của d không thuộc (α).
Vậy d // (α)
Chọn A.
3.80
Cho đường thẳng \(d:\dfrac{{x - 1}}{1} = \dfrac{{y - 1}}{2} = \dfrac{{z - 2}}{{ - 3}}\) và mặt phẳng (α): x + y + z - 4 = 0
Khẳng định nào sau đây là đúng?
A. d cắt (α) B. d // (α)
C. d ⊂ (α) D. d ⊥ (α)
Lời giải chi tiết:
Đường thẳng d có vectơ chỉ phương là \(\overrightarrow u = \left( {1;2; - 3} \right)\)
Mặt phẳng (α) có vectơ pháp tuyến \(\overrightarrow n = \left( {1;1;1} \right)\)
Ta thấy: \(\overrightarrow u .\overrightarrow n = 1.1 + 2.1 - 3.1 = 0\) nên \(\overrightarrow u \bot \overrightarrow n \)
Mà điểm cố định M(1; 1; 2) của d nằm trên (α). Vậy d ⊂ (α)
Chọn C.
3.81
Hãy tìm kết luận đúng về vị trí tương đối giữa hai đường thẳng:
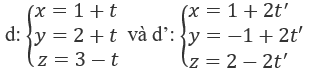
A. d cắt d' B. d ≡ d'
C. d chéo với d' D. d // d'
Lời giải chi tiết:
Ta thấy:
\(d\) có VTCP \(\overrightarrow {{u_1}} = \left( {1;1; - 1} \right)\) và đi qua \(M\left( {1;2;3} \right)\)
\(d'\) có VTCP \(\overrightarrow {{u_2}} = \left( {2;2; - 2} \right)\).
Có \(\overrightarrow {{u_2}} = 2\overrightarrow {{u_1}} \) và thay tọa độ của M vào \(d'\) ta được:
\(\left\{ \begin{array}{l}1 = 1 + 2t'\\2 = - 1 + 2t'\\3 = 3 - 2t'\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t' = 0\\t' = \dfrac{3}{2}\\t' = 0\end{array} \right.\left( {vo\,li} \right)\) nên \(M \notin d'\)
Hai đường thẳng d và d' có hai vectơ chỉ phương tỉ lệ và một điểm của đường này không nằm trên đường kia.
Suy ra d // d'.
Chọn D.
3.82
Giao điểm giữa hai đường thẳng:
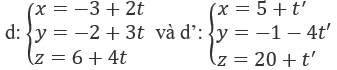
A. (-3; -2; 6) B. (5; -1; 20)
C. (3; 7; 18) D. (3; -2; 1)
Lời giải chi tiết:
Giải hệ phương trình: \(\left\{ \begin{array}{l} - 3 + 2t = 5 + t'\\ - 2 + 3t = - 1 - 4t'\\6 + 4t = 20 + t'\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2t - t' = 8\\3t + 4t' = 1\\4t - t' = 14\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}t = 3\\t' = - 2\end{array} \right.\)
Vậy giao điểm của d và d' là M(3; 7; 18).
Chọn C.
3.83
Tìm m để hai đường thẳng sau đây cắt nhau:
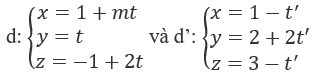
A. m = 0 B. m = 1
C. m = -1 D. m = 2
Lời giải chi tiết:
\(d\) có VTCP \(\overrightarrow u = \left( {m;1;2} \right)\) và đi qua M(1; 0; -1)
\(d'\) có VTCP \(\overrightarrow {u'} = \left( { - 1;2; - 1} \right)\) và đi qua M'(1; 2; 3)
Ta có: \(\overrightarrow {MM'} = \left( {0;2;4} \right)\), \(\left[ {\overrightarrow u ,\overrightarrow {u'} } \right] = \left( { - 2;m - 2;2m + 1} \right)\)
d và d' cắt nhau ⇔ \(\left[ {\overrightarrow u ,\overrightarrow {u'} } \right].\overrightarrow {MM'} = 0\)
⇔ 2(m - 2) + 4(2m + 1) = 0
⇔ m = 0
Chọn A.
3.84
Khoảng cách từ điểm M(-2; -4; 3) đến mặt phẳng (α): 2x - y + 2z - 3 = 0 là:
A. 3 B. 2
C. 1 D. 11
Lời giải chi tiết:
Ta có:
\(d\left( {M,\left( \alpha \right)} \right)\) \( = \dfrac{{\left| {2.\left( { - 2} \right) - \left( { - 4} \right) + 2.3 - 3} \right|}}{{\left| {{2^2} + {1^2} + {2^2}} \right|}}\) \( = \dfrac{3}{3} = 1\)
Chọn C.
3.85
Gọi H là hình chiếu vuông góc của điểm A(2; -1; -1) đến mặt phẳng (α): 16x - 12y - 15z - 4 = 0. Độ dài của đoạn AH là:
A. 55 B. 11/5
C. 11/25 D. 22/5
Lời giải chi tiết:
Ta có:
\(AH = d\left( {A,\left( \alpha \right)} \right)\)\( = \dfrac{{\left| {16.2 - 12.\left( { - 1} \right) - 15.\left( { - 1} \right) - 4} \right|}}{{\sqrt {{{16}^2} + {{12}^2} + {{15}^2}} }}\) \( = \dfrac{{55}}{{25}} = \dfrac{{11}}{5}\)
Chọn B.
3.86
Cho mặt cầu tâm I(4; 2; -2) bán kính r tiếp xúc với mặt phẳng (P): 12x - 5z - 19 = 0. Bán kính r bằng:
A. 39 B. 3
C. 13 D. 39/√(13)
Lời giải chi tiết:
Mặt cầu tâm I bán kính r tiếp xúc với mặt phẳng (P) khi
\(R = d\left( {I,\left( P \right)} \right)\)\( = \dfrac{{\left| {12.4 - 5.\left( { - 2} \right) - 19} \right|}}{{\sqrt {{{12}^2} + {5^2}} }}\) \( = \dfrac{{39}}{{13}} = 3\)
Chọn B.
3.87
Cho hai mặt phẳng song song: (α): x + y - z + 5 = 0 và (β): 2x + 2y - 2z + 3 = 0
Khoảng cách giữa (α) và (β) là:
A. 2/(√3) B. 2
C. 7/2 D. 7/(2√3)
Lời giải chi tiết:
Lấy điểm M(0; 0; 5) thuộc (α).
Do \(\left( \alpha \right)//\left( \beta \right)\) nên \(d\left( {\left( \alpha \right),\left( \beta \right)} \right) = d\left( {M,\left( \beta \right)} \right)\) \( = \dfrac{{\left| {2.0 + 2.0 - 2.5 + 3} \right|}}{{\sqrt {{2^2} + {2^2} + {2^2}} }} = \dfrac{7}{{2\sqrt 3 }}\)
Chọn D.
3.88
Khoảng cách từ điểm M(2; 0; 1) đến đường thẳng \(d:\dfrac{{x - 1}}{1} = \dfrac{y}{2} = \dfrac{{z - 2}}{1}\) là:
A. √(12) B. √3
C. √2 D. 12/(√6)
Lời giải chi tiết:
Lấy điểm A(1; 0; 2) trên d và một vectơ chỉ phương của d là \(\overrightarrow u = \left( {1;2;1} \right)\)
\(\overrightarrow {AM} = \left( {1;0; - 1} \right)\) \( \Rightarrow \left[ {\overrightarrow {AM} ,\overrightarrow u } \right] = \left( {2; - 2;2} \right)\)
\(d\left( {M,d} \right) = \dfrac{{\left| {\left[ {\overrightarrow {AM} ,\overrightarrow u } \right]} \right|}}{{\left| {\overrightarrow u } \right|}}\) \( = \dfrac{{\sqrt {{2^2} + {2^2} + {2^2}} }}{{\sqrt {{1^2} + {2^2} + {1^2}} }} = \sqrt 2 \)
Chọn C.
3.89
Bán kính của mặt cầu tâm I(1; 3; 5) và tiếp xúc với đường thẳng \(\left\{ \begin{array}{l}x = t\\y = - 1 - t\\z = 2 - t\end{array} \right.\) là:
A. √(14) B. 14
C. √7 D. 7
Lời giải chi tiết:
Đường thẳng \(d\) đi qua điểm \(A\left( {0; - 1;2} \right)\) và VTCP \(\overrightarrow u = \left( {1; - 1; - 1} \right)\).
\( \Rightarrow \overrightarrow {IA} = \left( { - 1; - 4; - 3} \right)\) \( \Rightarrow \left[ {\overrightarrow {IA} ,\overrightarrow u } \right] = \left( {1; - 4;5} \right)\)
\( \Rightarrow R = d\left( {I,d} \right) = \dfrac{{\left| {\left[ {\overrightarrow {IA} ,\overrightarrow u } \right]} \right|}}{{\left| {\overrightarrow u } \right|}}\) \( = \dfrac{{\sqrt {1 + {4^2} + {5^2}} }}{{\sqrt {{1^2} + {1^2} + {1^2}} }} = \sqrt {14} \)
Chọn A.
3.90
Khoảng cách giữa hai đường thẳng:
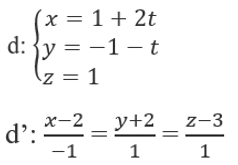
A. √6 B. (√6)/2
C. 1/(√6) D. √2
Lời giải chi tiết:
d đi qua điểm M(1; -1; 1) và có vectơ chỉ phương \(\overrightarrow u \) = (2; -1; 0);
d' đi qua điểm M'(2; -2; 3) và có vectơ chỉ phương \(\overrightarrow {u'} \) = (-1; 1; 1)
Ta có: \(\overrightarrow {MM'} = \left( {1; - 1;2} \right)\), \(\left[ {\overrightarrow u ,\overrightarrow {u'} } \right] = \left( { - 1; - 2;1} \right)\)
\(d\left( {d,d'} \right) = \dfrac{{\left| {\left[ {\overrightarrow u ,\overrightarrow {u'} } \right].\overrightarrow {MM'} } \right|}}{{\left| {\left[ {\overrightarrow u ,\overrightarrow {u'} } \right]} \right|}}\) \( = \dfrac{{\left| { - 1.1 - 2.\left( { - 1} \right) + 1.2} \right|}}{{\sqrt {{1^2} + {2^2} + {1^2}} }}\) \( = \dfrac{3}{{\sqrt 6 }} = \dfrac{{\sqrt 6 }}{2}\)
Ta được khoảng cách giữa hai đường thẳng d và d' bằng (√6)/2.
Chọn B.
3.91
Tọa độ hình chiếu vuông góc của điểm M(2; 0; 1) trên đường thẳng \(\Delta :\dfrac{{x - 1}}{1} = \dfrac{y}{2} = \dfrac{{z - 2}}{1}\)
A. (1; 0; 2) B. (2; 2; 3)
C. (0; -2; 1) D. (-1; -4; 0)
Lời giải chi tiết:
Đường thẳng \(\Delta :\dfrac{{x - 1}}{1} = \dfrac{y}{2} = \dfrac{{z - 2}}{1}\) có phương trình tham số là: \(\left\{ \begin{array}{l}x = 1 + t\\y = 2t\\z = 2 + t\end{array} \right.\).
Gọi H(1 + t; 2t; 2 + t) là một điểm trên Δ \( \Rightarrow \overrightarrow {MH} = \left( { - 1 + t;2t;1 + t} \right)\)
\(\Delta \) có VTCP \(\overrightarrow {{u_\Delta }} = \left( {1;2;1} \right)\)
H là hình chiếu vuông góc của M trên Δ \( \Leftrightarrow \overrightarrow {MH} .\overrightarrow {{u_\Delta }} = 0\)
\(\begin{array}{l} \Leftrightarrow 1.\left( { - 1 + t} \right) + 2.2t + 1.\left( {1 + t} \right) = 0\\ \Leftrightarrow - 1 + t + 4t + 1 + t = 0\\ \Leftrightarrow t = 0\end{array}\)
Suy ra H(1; 0; 2)
Chọn A.
3.92
Cho mặt phẳng (α): 3x - 2y - z + 5 = 0 và đường thẳng \(\Delta :\dfrac{{x - 1}}{2} = \dfrac{{y - 7}}{1} = \dfrac{{z - 3}}{4}\)
Gọi (β) là mặt phẳng chứa Δ và song song với (α). Khoảng cách giữa (α) và (β) là:
A. 9/14 B. 9/(√(14))
C. 3/14 D. 3/(√(14))
Lời giải chi tiết:
Lấy điểm \(M\left( {1;7;3} \right) \in \Delta \subset \left( \beta \right)\)
Do \(\left( \beta \right)//\left( \alpha \right)\) nên \(d\left( {\left( \beta \right),\left( \alpha \right)} \right) = d\left( {M,\left( \alpha \right)} \right)\)
Ta có: \(d\left( {M,\left( \alpha \right)} \right) = \dfrac{{\left| {3.1 - 2.7 - 3 + 5} \right|}}{{\sqrt {{3^2} + {2^2} + {1^2}} }}\) \( = \dfrac{9}{{\sqrt {14} }}\)
Chọn B.

