Đề bài
Chứng minh rằng tổng các khoảng cách từ một điểm bất kì trong một tứ diện đều đến các mặt của nó là một số không đổi.
Phương pháp giải - Xem chi tiết
- Tính thể tích mỗi khối chóp đỉnh \(M\) và đáy là các tam giác đều.
- Tính tổng thể tích và suy ra tổng khoảng cách từ \(M\) đến các mặt bên.
Lời giải chi tiết
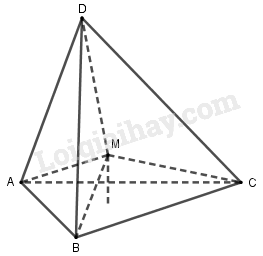
Xét tứ diện đều \(ABCD\), \(M\) là một điểm trong của nó.
Gọi \(V\) là thể tích, \(S\) là diện tích mỗi mặt của tứ diện đều \(ABCD\), \({h_A},{h_B},{h_C},{h_D}\) lần lượt là khoảng cách từ \(M\) đến các mặt \(\left( {BCD} \right),\left( {CDA} \right),\left( {DAB} \right),\left( {ABC} \right)\).
Ta có: \({V_{M.BCD}} = \dfrac{1}{3}S{h_A},{V_{M.CDA}} = \dfrac{1}{3}S{h_B},\) \({V_{M.DAB}} = \dfrac{1}{3}S{h_C},{V_{M.ABC}} = \dfrac{1}{3}S{h_D}\)
Khi đó ta có \(V = {V_{MBCD}} + {V_{MCDA}} + {V_{MDAB}} + {V_{MABC}}\)\( = \dfrac{1}{3}S\left( {{h_A} + {h_B} + {h_C} + {h_D}} \right)\)
\( \Rightarrow {h_A} + {h_B} + {h_C} + {h_D} = \dfrac{{3V}}{S}\).
Mà \(V,S\) là các số không đổi nên \({h_A} + {h_B} + {h_C} + {h_D}\) không đổi. (đpcm)

