Đề bài
Cho tứ diện \(ABCD\). Gọi \({h_A},{h_B},{h_C},{h_D}\;\) lần lượt là các đường cao của tứ diện xuất phát từ A, B, C, D và r là bán kính mặt cầu nội tiếp tứ diện. Chứng minh rằng: \(\dfrac{1}{{{h_A}}} + \dfrac{1}{{{h_B}}} + \dfrac{1}{{{h_C}}} + \dfrac{1}{{{h_D}}} = \dfrac{1}{r}\)
Phương pháp giải - Xem chi tiết
- Chia khối tứ diện thành bốn khối tứ diện nhỏ có đỉnh là tâm mặt cầu nội tiếp tứ diện và đáy là các mặt của tứ diện.
- Tính tỉ số thể tích mỗi khối tứ diện so với thể tích khối tứ diện \(ABCD\) và cộng vế với vế suy ra điều phải chứng minh.
Lời giải chi tiết
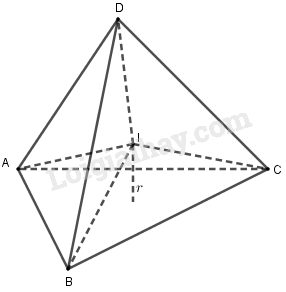
Gọi \(I\) là tâm mặt cầu nội tiếp tứ diện, \(V\)là thể tích tứ diện.
Ta có \({V_{I.BCD}} = \dfrac{1}{3}{S_{BCD}}.r\); \({V_{I.CDA}} = \dfrac{1}{3}{S_{CDA}}.r\); \({V_{I.DAB}} = \dfrac{1}{3}{S_{DAB}}.r\); \({V_{I.ABC}} = \dfrac{1}{3}{S_{ABC}}.r\)
\(V = {V_{IBCD}} + {V_{ICDA}} + {V_{IDAB}} + {V_{IABC}}\)
\( \Rightarrow \frac{V}{V} = \frac{{{V_{IBCD}} + {V_{ICDA}} + {V_{IDAB}} + {V_{IABC}}}}{V}\)
\( \Rightarrow 1 = \dfrac{{{V_{IBCD}}}}{V} + \dfrac{{{V_{ICDA}}}}{V} + \dfrac{{{V_{IDAB}}}}{V} + \dfrac{{{V_{IABC}}}}{V}\)
\( = \dfrac{{\dfrac{1}{3}r{S_{BCD}}}}{{\dfrac{1}{3}{h_A}{S_{BCD}}}} + \dfrac{{\dfrac{1}{3}r{S_{CDA}}}}{{\dfrac{1}{3}{h_B}{S_{CDA}}}}\) \( + \dfrac{{\dfrac{1}{3}r{S_{DAB}}}}{{\dfrac{1}{3}{h_C}{S_{DAB}}}} + \dfrac{{\dfrac{1}{3}r{S_{ABC}}}}{{\dfrac{1}{3}{h_D}{S_{ABC}}}}\)
\( = r\left( {\dfrac{1}{{{h_A}}} + \dfrac{1}{{{h_B}}} + \dfrac{1}{{{h_C}}} + \dfrac{1}{{{h_D}}}} \right)\)
\( \Rightarrow 1 = r\left( {\frac{1}{{{h_A}}} + \frac{1}{{{h_B}}} + \frac{1}{{{h_C}}} + \frac{1}{{{h_D}}}} \right)\)
\( \Rightarrow \dfrac{1}{r} = \dfrac{1}{{{h_A}}} + \dfrac{1}{{{h_B}}} + \dfrac{1}{{{h_C}}} + \dfrac{1}{{{h_D}}}\) (đpcm).

