Đề bài
Cho hai đoạn thẳng \(AB\) và \(CD\) chéo nhau, \(AC\) là đường vuông góc chung của chúng. Biết rằng \(AC = h, AB = a, CD = b\) và góc giữa hai đường thẳng \(AB\) và \(CD\) bằng \({60^0}\). Hãy tính thể tích của khối tứ diện \(ABCD\).
Phương pháp giải - Xem chi tiết
- Dựng hình hình bình hành \(CDBE\) và \(ABDF\).
- Tính thể tích tứ diện \(ABCE\) rồi suy ra thể tích khối tứ diện \(ABCD\).
Lời giải chi tiết
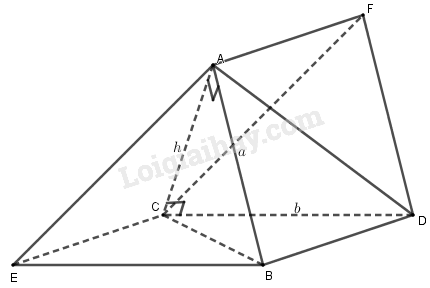
Dựng hình hình bình hành \(CDBE\) và \(ABDF\).
Khi đó, \(ABE.FDC\) là hình lăng trụ.
Ta có: \(AC \bot CD,CD//BE\) \( \Rightarrow AC \bot BE\), mà \(AC \bot AB\) nên \(AC \bot \left( {ABE} \right)\).
Lại có \(\widehat {\left( {AB,CD} \right)} = \widehat {\left( {AB,BE} \right)}\) \( = \widehat {ABE} = {60^0}\)
\( \Rightarrow {S_{ABE}} = \dfrac{1}{2}AB.BE.\sin \widehat {ABE}\)\( = \dfrac{1}{2}ab.\sin {60^0} = \dfrac{{ab\sqrt 3 }}{4}\)
\( \Rightarrow {V_{C.ABE}} = \dfrac{1}{3}{S_{ABE}}.AC\)\( = \dfrac{1}{3}.\dfrac{{ab\sqrt 3 }}{4}.h = \dfrac{{abh\sqrt 3 }}{{12}}\)
Từ đó suy ra \({V_{A.BCD}} = {V_{A.BCE}} = \dfrac{{abh\sqrt 3 }}{{12}}\).

