Cho hàm số: \(y = \dfrac{{2x + 1}}{{x - 2}}\).
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b) Viết phương trình tiếp tuyến của đồ thị (C) , biết hệ số góc của tiếp tuyến bằng \( - 5\).
(Đề thi tốt nghiệp THPT năm 2009)
LG a
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho
Phương pháp giải:
- Tìm TXĐ.
- Xét sự biến thiên.
- Vẽ đồ thị hàm số.
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\).
Có \(y' = \dfrac{{ - 5}}{{{{\left( {x - 2} \right)}^2}}} < 0,\forall x \in D\) nên hàm số nghịch biến trên các khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).
Giới hạn: \(\mathop {\lim }\limits_{x \to \pm \infty } y = 2\) nên TCN \(y = 2\).
\(\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty ,\mathop {\lim }\limits_{x \to {2^ - }} y = - \infty \) nên TCĐ \(x = 2\).
Bảng biến thiên:
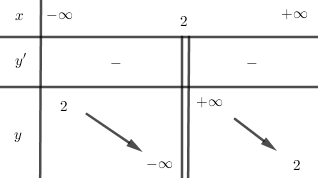
Đồ thị:
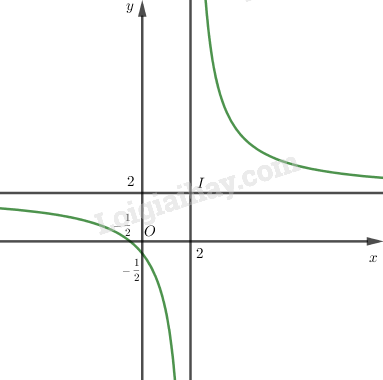
LG b
Viết phương trình tiếp tuyến của đồ thị (C) , biết hệ số góc của tiếp tuyến bằng \( - 5\).
Phương pháp giải:
- Giải phương trình \(y' = k\) tìm hoành độ giao điểm.
- Viết phương trình tiếp tuyến theo công thức \(y = k\left( {x - {x_0}} \right) + {y_0}\).
Lời giải chi tiết:
Ta có: \(y' = \dfrac{{ - 5}}{{{{\left( {x - 2} \right)}^2}}} = - 5\)\( \Leftrightarrow {(x - 2)^2} = 1\) \( \Leftrightarrow \left[ \begin{array}{l}x - 2 = 1\\x - 2 = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)
Với \(x = 3\) ta có \(y = 7\) nên phương trình tiếp tuyến là \(y = - 5\left( {x - 3} \right) + 7\) hay \(y = - 5x + 22\).
Với \(x = 1\) ta có \(y = - 3\) nên phương trình tiếp tuyến là \(y = - 5\left( {x - 1} \right) - 3\) hay \(y = - 5x + 2\).

