Đề bài
Cho hình chóp tam giác đều \(S.ABC\) có cạnh đáy bằng \(a\) và khoảng cách từ trọng tâm tam giác \(ABC\) đến mặt bên \(\left( {SAB} \right)\) bằng \(\dfrac{a}{4}\). Thể tích của hình chóp bằng:
A. \(\dfrac{{\sqrt 3 }}{{24}}{a^3}\) B. \(\dfrac{{\sqrt 3 }}{{16}}{a^3}\)
C. \(\dfrac{{\sqrt 3 }}{{12}}{a^3}\) D. \(\dfrac{{\sqrt 2 }}{{12}}{a^3}\)
Phương pháp giải - Xem chi tiết
- Dựng hình chiếu của trọng tâm tam giác \(ABC\) trên mặt phẳng \(\left( {SAB} \right)\).
- Tính chiều cao và diện tích đáy của hình chóp.
- Tính thể tích theo công thức \(V = \dfrac{1}{3}Sh\).
Lời giải chi tiết
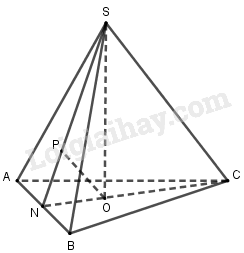
Gọi \(N\) là trung điểm của \(AB\), \(O\) là trọng tâm tam giác \(ABC\), \(P\) là hình chiếu của \(O\) lên \(AN\).
Dễ thấy \(SO \bot \left( {ABC} \right) \Rightarrow SO \bot AB\), mà \(AB \bot CN\) nên \(AB \bot \left( {SNC} \right) \Rightarrow AB \bot OP\).
Lại có \(OP \bot SN\) nên \(OP \bot \left( {SAB} \right)\) hay \(d\left( {O,\left( {SAB} \right)} \right) = OP = \dfrac{a}{4}\).
Ta có: \(CN = \dfrac{{a\sqrt 3 }}{2}\) \( \Rightarrow ON = \dfrac{1}{3}CN = \dfrac{{a\sqrt 3 }}{6}\).
Tam giác \(SON\) vuông tại \(O\) có \(\dfrac{1}{{O{P^2}}} = \dfrac{1}{{O{N^2}}} + \dfrac{1}{{S{O^2}}}\) \( \Rightarrow \dfrac{{16}}{{{a^2}}} = \dfrac{{36}}{{3{a^2}}} + \dfrac{1}{{S{O^2}}} \Rightarrow SO = \dfrac{a}{2}\).
Diện tích tam giác \(ABC\) là \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\).
Thể tích khôi chóp \({V_{S.ABC}} = \dfrac{1}{3}SO.{S_{ABC}}\) \( = \dfrac{1}{3}.\dfrac{a}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{{24}}\).
Chọn A.

