Đề bài
Cho tứ diện SABC có cạnh SA vuông góc với mặt phẳng (ABC) và có SA = a, AB = b , AC = c . Xác định tâm và bán kính hình cầu ngoại tiếp tứ diện trong các trường hợp sau:
a) ^BAC=900
b) ^BAC=600 và b=c
c) ^BAC=1200 và b=c
Phương pháp giải - Xem chi tiết
- Dựng tâm hình cầu (giao điểm của trục đường tròn ngoại tiếp tam giác ABC và trung trực của đoạn thẳng SA)
- Tính bán kính dựa vào các kiến thức hình học đã biết.
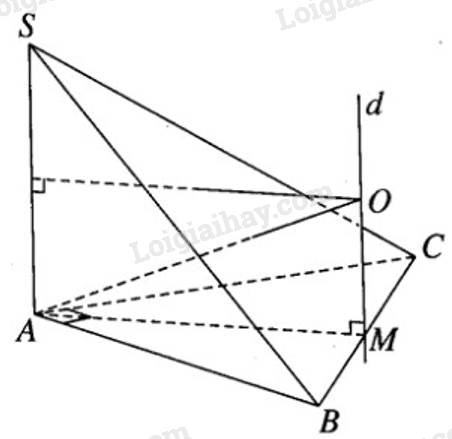
Lời giải chi tiết
^BAC=900. Gọi M là trung điểm của BC, ta có MA = MB = MC. Dựng đường thẳng d vuông góc với mặt phẳng (ABC) tại M. Mặt phẳng trung trực của đoạn SA cắt d tại O.
Ta có OS = OA = OB = OC
Và r2=OA2=OM2+MA2=(a2)2+(b2)2+(c2)2
Do đó ta có hình cầu tâm O ngoại tiếp tứ diện và có r=12√a2+b2+c2
b) ^BAC=600 và b = c, khi đó ABC là tam giác đều cạnh b. Gọi I là trọng tâm của tam giác đều nên I đồng thời cũng là tâm của đường tròn ngoại tiếp tam giác đều ABC. Dựng d là đường thẳng vuông góc với mặt phẳng (ABC) tại I. Mặt phẳng trung trực của đoạn SA cắt d tại O.
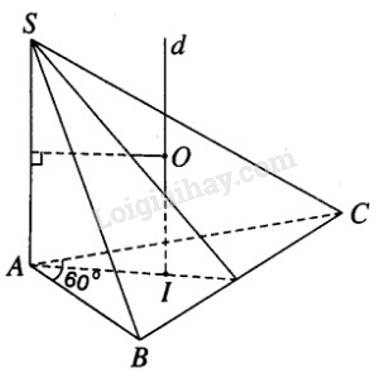
Ta có OS = OA = OB = OC và r2 = OA2 = OI2 + IA2
Do đó ta có hình cầu tâm O ngoại tiếp tứ diện và có
r2=(a2)2+(23b√32)2=a24+b23 . Vậy r=√a24+b23
c) ^BAC=1200 và b = c, khi đó ABC là một tam giác cân có góc A ở đỉnh bằng 1200 và cạnh bên bằng b. Gọi M là trung điểm của cạnh BC. Kéo dài AM một đoạn MK = AM, ta có KA = KB = KC = AB = AC = b.
Dựng đường thẳng d vuông góc với mặt phẳng (ABC) tại K. Mặt phẳng trung trực của đoạn SA cắt d tại O.
Ta có: OS = OA = OB = OC và r2=OA2=OK2+KA2=(a2)2+b2
Do đó ta có mặt cầu tâm O ngoại tiếp tứ diện và có bán kính r=√a24+b2
