Tính diện tích của hình phẳng giới hạn bởi các đường sau:
LG a
y = |x2 – 1| và y = 5 + |x|
Lời giải chi tiết:
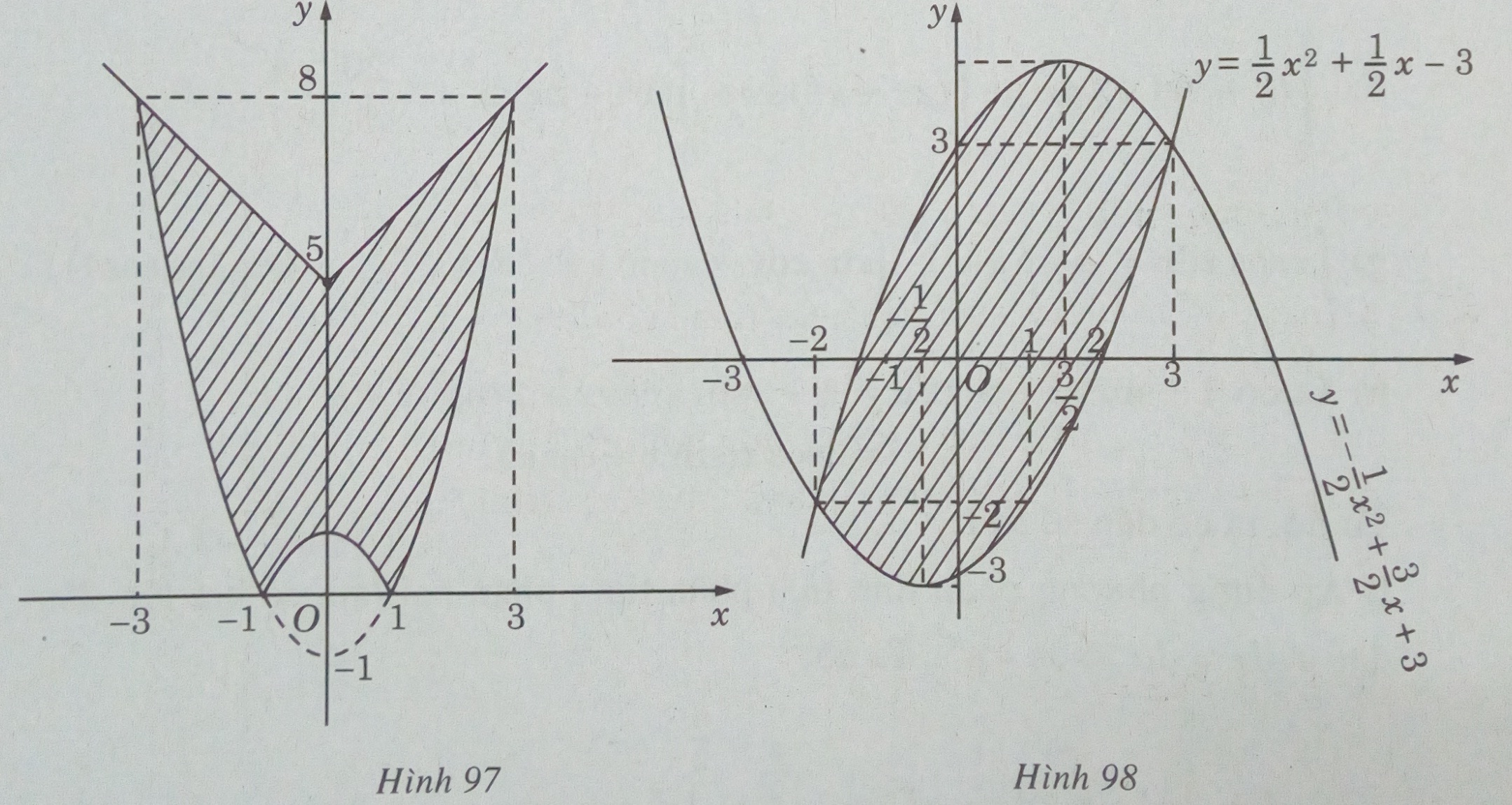
Hai hàm số y = |x2 – 1| và y = 5 + |x| đều là hàm số chẵn. Miền cần tính diện tích được thể hiện ở hình 97. Do tính đối xứng qua trục tung, ta có:
\(S = 2\int\limits_0^3 {(5 + |x| - |{x^2} - 1|)dx}\)
\( = 2\left[ {\int\limits_0^1 {(5 + x - 1 + {x^2})dx + \int\limits_1^3 {(5 + x - {x^2} + 1)dx} } } \right]\)
\( = 2\left[ {({1 \over 3}{x^3} + {1 \over 2}{x^2} + 4x)\left| {\matrix{1 \cr 0 \cr} + ( - {1 \over 3}{x^3} + {1 \over 2}{x^2} + 6x)\left| {\matrix{3 \cr 1 \cr} } \right.} \right.} \right]\)
\(= 24{1 \over 3}\) (đơn vị diện tích)
LG b
2y = x2 + x – 6 và 2y = -x2 + 3x + 6
Lời giải chi tiết:
Miền cần tính diện tích được thể hiện bởi Hình 98 (học sinh tự làm)
Như vậy, với mọi \(x \in ( - 2;3)\) đồ thị của hàm số \(y = - {1 \over 2}{x^2} + {3 \over 2}x + 3\) nằm phía trên đồ thị của hàm số \(y = {1 \over 2}{x^2} + {1 \over 2}x - 3\).
Vậy ta có:
\(S = \int\limits_{ - 2}^3 {\left[ {( - {1 \over 2}{x^2} + {3 \over 2}x + 3) - ({1 \over 2}{x^2} + {1 \over 2}x - 3)} \right]} dx\)
\(= \int\limits_{ - 2}^3 {( - {x^2} + x + 6)} dx = 20{5 \over 6}\) (đơn vị diện tích)
LG c
\(y = {1 \over x} + 1,x = 1\) và tiếp tuyến với đường \(y = {1 \over x} + 1\) tại điểm \((2;{3 \over 2})\)
Lời giải chi tiết:
Miền cần tính diện tích được thể hiện trên hình:
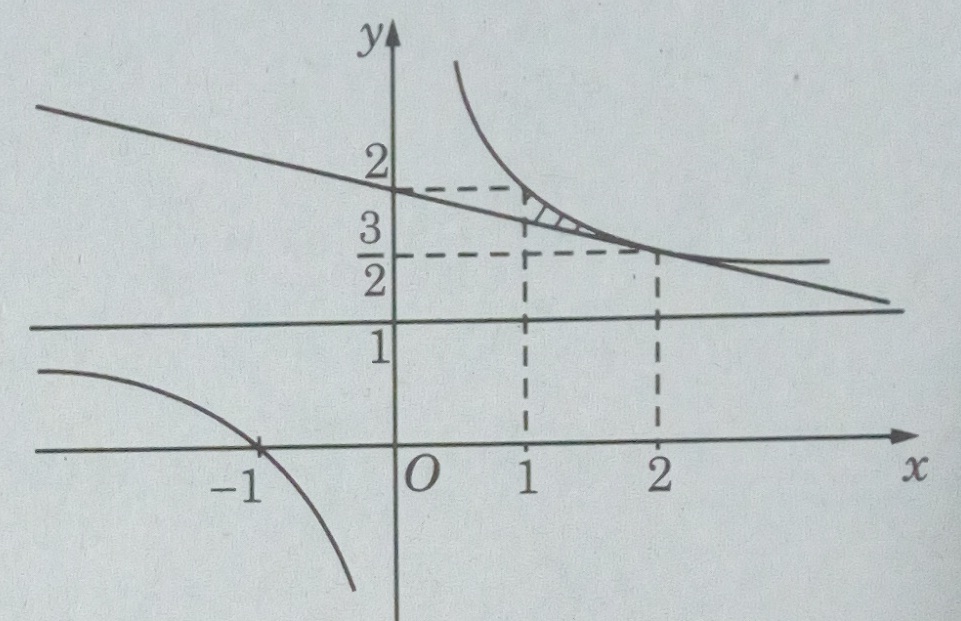
\(S = \int\limits_1^2 {\left[ {{1 \over x} + 1 - ( - {1 \over 4}x + 2)} \right]} dx\)
\(= \int\limits_1^2 {({1 \over x} + {1 \over 4}x - 1)dx = \ln 2 - {5 \over 8}} \)(đơn vị diện tích)
(vì tiếp tuyến với đồ thị của \(y = {1 \over x} + 1\) tại điểm \((2;{3 \over 2})\) có phương trình là \(y = f'(2)(x - 2) + {3 \over 2} = - {1 \over 4}x + 2\))

