Đề bài
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Bằng phương pháp tọa độ hãy tính khoảng cách giữa hai đường thẳng CA’ và DD’.
Phương pháp giải - Xem chi tiết
- Chọn hệ trục tọa độ gốc \(C\left( {0;0;0} \right)\) và xác định tọa độ các điểm còn lại.
- Viết phương trình mặt phẳng chứa \(CA'\) và song song \(DD'\).
- Tính khoảng cách \(d\left( {CA',DD'} \right) = d\left( {DD',\left( \alpha \right)} \right) = d\left( {D,\left( \alpha \right)} \right)\)
Lời giải chi tiết
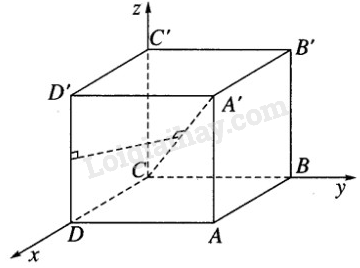
Ta chọn hệ trục tọa độ sao cho: C là gốc tọa độ, \(\overrightarrow {CD} = a\overrightarrow i ;\overrightarrow {CB} = a\overrightarrow j ;\overrightarrow {CC'} = a\overrightarrow k \)
Trong hệ tọa độ vừa chọn ta có: C(0; 0; 0), A’(a; a ; a), D(a,; 0;0), D’(a; 0; a)
\(\overrightarrow {CA'} = (a;a;a),\overrightarrow {{\rm{DD}}'} = (0;0;a)\)
Gọi \((\alpha )\) là mặt phẳng chứa \(\overrightarrow {CA'} \) và song song với \(\overrightarrow {DD'} \).
Mặt phẳng \((\alpha )\) có vecto pháp tuyến là: \(\overrightarrow n = \left[ {\overrightarrow {CA'} ,\overrightarrow {{\rm{DD}}'} } \right] = ({a^2}; - {a^2};0)\) hay x – y = 0
Phương trình tổng quát của \((\alpha )\) là x – y = 0.
Ta có: \(d\left( {CA',DD'} \right) = d\left( {D,\left( \alpha \right)} \right)\) \( = \dfrac{{\left| { - a} \right|}}{{\sqrt {1 + 1 + 0} }} = \dfrac{a}{{\sqrt 2 }}\).

