Đề bài
Hãy biểu diễn các số phức \(z\) trên mặt phẳng tọa độ, biết \(\left| z \right|\; \le 2\) và:
a) Phần thực của \(z\) không vượt quá phần ảo của nó;
b) Phần ảo của \(z\) lớn hơn \(1\);
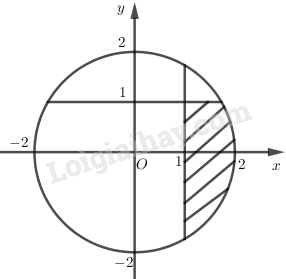
c) Phần ảo của \(z\) nhỏ hơn \(1\), phần thực của \(z\) lớn hơn \(1\).
Phương pháp giải - Xem chi tiết
Dựng đường tròn \({x^2} + {y^2} = 4\) và suy ra phần mặt phẳng biểu diễn các số phức theo yêu cầu.
Lời giải chi tiết
a) Vẽ đường tròn \({x^2} + {y^2} = 4\).
Phần thực không vượt quá phần ảo hay \(x \le y\).
Dựng đường thẳng \(y = x\), dễ thấy điểm \(\left( {0;2} \right)\) thuộc miền cần tìm (miền gạch sọc) nên ta có hình vẽ sau:

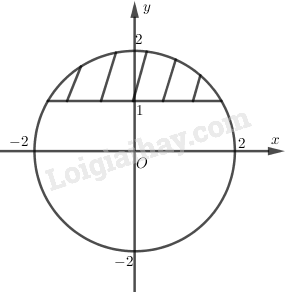
b) Phần ảo của \(z\) lớn hơn \(1\) hay \(y > 1\).
Ta có hình vẽ (phần gạch sọc là phần cần tìm).
c) Phần ảo của \(z\) nhỏ hơn \(1\), phần thực của \(z\) lớn hơn \(1\) hay \(x > 1,y < 1\).