Đề bài
Cho hình hộp \(ABCD.A’B’C’D’\). Tính \(\dfrac{{{V_{ACB'D'}}}}{{{V_{ABCD.A'B'C'D'}}}}\)
Phương pháp giải - Xem chi tiết
Tính thể tích khối hộp và thể tích tứ diện. Từ đó suy ra tỉ số.
Sử dụng phương pháp phân chia khối đa diện.
Lời giải chi tiết
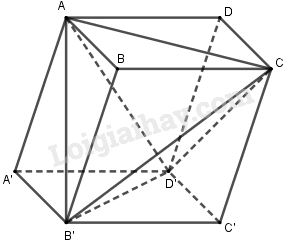
Đặt \(V = {V_{ABCD.A'B'C'D'}}\).
Ta có: \({V_{ACB'D'}} = V - {V_{A.A'B'D'}}\) \( - {V_{B'.BAC}} - {V_{C.C'B'D'}} - {V_{D'.ADC}}\)
Mà \({V_{A.A'B'D'}} = {V_{B'.BAC}}\) \( = {V_{C.C'B'D'}} = {V_{D'.ADC}} = \dfrac{1}{6}V\)
\( \Rightarrow {V_{ACB'D'}} = V - \dfrac{4}{6}V = \dfrac{1}{3}V\).
Vậy \(\dfrac{{{V_{ACB'D'}}}}{{{V_{ABCD.A'B'C'D'}}}} = \dfrac{1}{3}\).

