LG a
Xác định a, b, c, d để đồ thị của các hàm số: y = x2 + ax + b và y = cx + d cùng đi qua hai điểm M(1; 1) và B(3; 3).
Lời giải chi tiết:
a và b thỏa mãn hệ phương trình :
\(\left\{ {\matrix{{1 + a + b = 1} \cr {9 + 3a + b = 3} \cr} } \right. \Leftrightarrow \left\{ {\matrix{{a + b = 0} \cr {3a + b = - 6} \cr} } \right. \Leftrightarrow\left\{ {\matrix{{a = - 3} \cr {b = 3} \cr} } \right.\)
c và d thỏa mãn hệ phương trình:
\(\left\{ {\matrix{{c + d = 1} \cr {3c + d = 3} \cr} \Leftrightarrow \left\{ {\matrix{{c = 1} \cr {d = 0} \cr} } \right.} \right.\)
LG b
Vẽ đồ thị của các hàm số ứng với các giá trị a, b, c và d tìm được trên cùng một mặt phẳng tọa độ. Tính diện tích của hình phẳng giới hạn bởi hai đường cong trên.
Lời giải chi tiết:
(H.90) Ta có hai hàm số tương ứng là: y = x2 – 3x + 3 và y = x
Vậy \(S = \int\limits_1^3 {\left[ {x - \left( {{x^2} - 3x + 3} \right)} \right]dx} \) \( = \int\limits_1^3 {\left( { - {x^2} + 4x - 3} \right)dx} \) \( = \left. {\left( { - \dfrac{{{x^3}}}{3} + 2{x^2} - 3x} \right)} \right|_1^3 \) \( = 0 - \left( { - \dfrac{4}{3}} \right) = \dfrac{4}{3}\) (đơn vị diện tích)
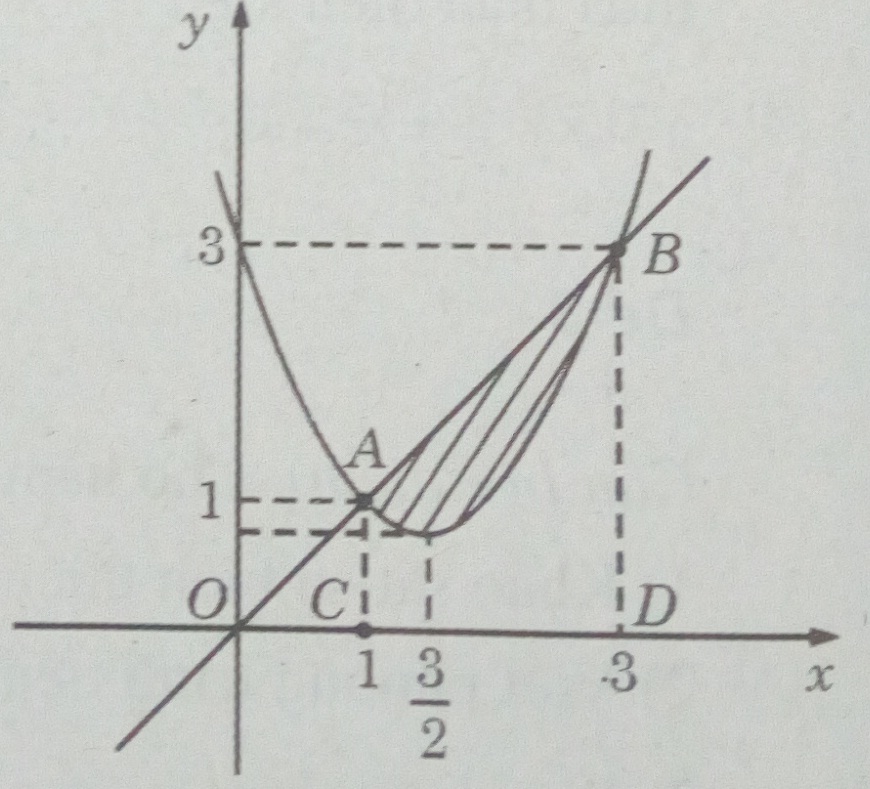
LG c
Tính thể tích của vật thể tròn xoay sinh bởi hình phẳng trên quay quanh trục hoành.
Lời giải chi tiết:
V = V1 – V2 , trong đó V1 là thể tích vật thể tròn xoay sinh ra do quay hình thang ACDB quanh trục Ox , V2 là thể tích vật thể tròn xoay sinh ra do quay hình thang cong ACDB quanh trục Ox.
Ta có:
\({V_1} = \pi \int\limits_1^3 {{x^2}dx} = \pi .\left. {\dfrac{{{x^3}}}{3}} \right|_1^3 \) \(= \pi \left( {9 - \dfrac{1}{3}} \right) = \dfrac{{26\pi }}{3}\)
\({V_2} = \pi \int\limits_1^3 {{{\left( {{x^2} - 3x + 3} \right)}^2}dx} \) \( = \pi \int\limits_1^3 {\left( {{x^4} + 9{x^2} + 9 - 6{x^3} - 18x + 6{x^2}} \right)dx} \) \( = \pi \int\limits_1^3 {\left( {{x^4} - 6{x^3} + 15{x^2} - 18x + 9} \right)dx} \) \( = \left. {\pi \left( {\dfrac{{{x^5}}}{5} - \dfrac{{6{x^4}}}{4} + \dfrac{{15{x^3}}}{3} - \dfrac{{18{x^2}}}{2} + 9x} \right)} \right|_1^3\) \( = \pi \left( {\dfrac{{81}}{{10}} - \dfrac{{37}}{{10}}} \right) = \dfrac{{22\pi }}{5}\)
Vậy \(V = {{26} \over 3}\pi - {{22} \over 5}\pi = {{64} \over {15}}\pi \) (đơn vị thể tích)

