Đề bài
Cho khối chóp tam giác đều \(S.ABC\) có đáy là tam giác đều cạnh bằng \(a\), các cạnh bên tạo với đáy một góc \({60^0}\). Hãy tính thể tích của khối chóp đó.
Phương pháp giải - Xem chi tiết
- Tính chiều cao và diện tích tam giác đáy.
- Tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\).
Lời giải chi tiết
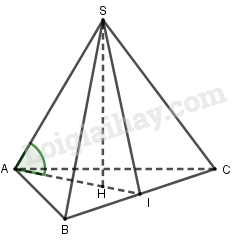
Kẻ \(SH \bot (ABC)\). Đường thẳng \(AH\) cắt \(BC\) tại \(I\).
Do \(S.ABC\) là hình chóp tam giác đều nên \(H\) là trọng tâm của \(\Delta ABC\) nên I là trung điểm BC.
Nên AI vừa là trung tuyến vừa là đường cao trong tam giác.
Tam giác ABI vuông tại I có \(AB = a,BI = \frac{a}{2}\).
Theo Pitago ta có: \(AI = \sqrt {A{B^2} - B{I^2}} \) \(= \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
Do đó \(AH = \frac{2}{3}AI= \dfrac{2}{3}.\frac{{a\sqrt 3 }}{2} = \dfrac{{\sqrt 3 }}{3}a,\)
Ta có: \(SH \bot \left( {ABC} \right)\) nên AH là hình chiếu của SA trên mp(ABC)
Do đó góc giữa SA và (ABC) là góc giữa SA và AH hay \(\widehat {SAH} = {60^0}\)
Tam giác SAH vuông tại H có \(SH = AH.\tan {60^0} = \dfrac{{\sqrt 3 }}{3}a.\sqrt 3 = a\)
Thể tích khối chóp \(S.ABC\) là:
\(V = \frac{1}{3}SH.{S_{ABC}}= \frac{1}{3}SH.\frac{1}{2}AI.BC\) \( = \frac{1}{3}.a.\frac{1}{2}.\frac{{a\sqrt 3 }}{2}.a= \dfrac{{\sqrt 3 }}{{12}}{a^3}\).

