Cho hàm số: \(y = {x^3} - (m + 4){x^2} - 4x + m\) (1)
LG a
Tìm các điểm mà đồ thị của hàm số (1) đi qua với mọi giá trị của \(m\).
Phương pháp giải:
- Biến đổi hàm số về phương trình ẩn \(m\) với tham số là \(x,y\).
- Cho các hệ số của \(m\) và hệ số tự do bằng \(0\) rồi tìm \(x,y\) và kết luận.
Lời giải chi tiết:
Ta có: \(y = {x^3} - (m + 4){x^2} - 4x + m\)
\(\begin{array}{l}
\Leftrightarrow y = {x^3} - m{x^2} - 4{x^2} - 4x + m\\
\Leftrightarrow y - {x^3} + m{x^2} + 4{x^2} + 4x - m = 0\\
\Leftrightarrow \left( {m{x^2} - m} \right) + y - {x^3} + 4{x^2} + 4x = 0
\end{array}\)
\( \Leftrightarrow \left( {{x^2} - 1} \right)m + y - {x^3} + 4{x^2} + 4x = 0\)
Đồ thị của hàm số (1) luôn luôn đi qua điểm \(A\left( {x;y} \right)\) với mọi \(m\) khi \(\left( {x;y} \right)\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}{x^2} - 1 = 0\\y - {x^3} + 4{x^2} + 4x = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = \pm 1\\y = {x^3} - 4{x^2} - 4x\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = 1,y = - 7\\x = - 1;y = - 1\end{array} \right.\)
Vậy đồ thị của hàm số luôn luôn đi qua hai điểm \(\left( {1; - 7} \right)\) và \(\left( { - 1; - 1} \right).\)
LG b
Chứng minh rằng với mọi giá trị của \(m\), đồ thị của hàm số (1) luôn luôn có cực trị.
Phương pháp giải:
Hàm số đa thức bậc ba luôn có cực trị nếu \(y' = 0\) luôn có hai nghiệm phân biệt với \(\forall m\).
Lời giải chi tiết:
Ta có: \(y' = 3{x^2} - 2(m + 4)x - 4\); \(\Delta ' = {(m + 4)^2} + 12 > 0,\forall m\)
Do dó phương trình \(y' = 0\) luôn luôn có hai nghiệm phân biệt (và đổi dấu khi qua hai nghiệm đó).
Từ đó suy ra đồ thị của (1) luôn luôn có cực trị.
LG c
Khảo sát sự biến thiên và vẽ đồ thị (C) của (1) khi \(m = 0\)
Phương pháp giải:
Khảo sát tóm tắt:
+ Thay \(m = 0\) vào hàm số đã cho.
+ Tính \(y'\).
+ Lập bảng biến thiên và vẽ đồ thị hàm số.
Lời giải chi tiết:
Với \(m = 0\) ta được hàm số \(y = {x^3} - 4{x^2} - 4x\).
TXĐ: \(D = \mathbb{R}\)
Chiều biến thiên:
\(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \)
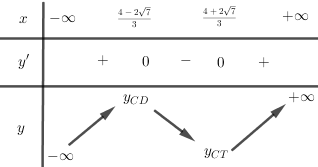
Có \(y' = 3{x^2} - 8x - 4\), \(y' = 0 \Leftrightarrow x = \dfrac{{4 \pm 2\sqrt 7 }}{3}\)
Hàm số đồng biến trên các khoảng \(\left( { - \infty ;\frac{{4 - 2\sqrt 7 }}{3}} \right)\) và \(\left( {\frac{{4 + 2\sqrt 7 }}{3}; + \infty } \right)\)
Hàm số nghịch biến trên khoảng \(\left( {\frac{{4 - 2\sqrt 7 }}{3};\frac{{4 + 2\sqrt 7 }}{3}} \right)\)
Hàm số đạt cực đại tại \(x = \frac{{4 - 2\sqrt 7 }}{3}\), đạt cực tiểu tại \(x = \frac{{4 + 2\sqrt 7 }}{3}\)
Bảng biến thiên:
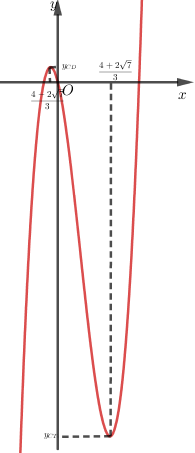
Đồ thị:
LG d
Xác định \(k\) để (C) cắt đường thẳng \(y = kx\) tại ba điểm phân biệt.
Phương pháp giải:
- Giải phương trình hoành độ giao điểm tìm nghiệm đặc biệt.
- Từ đó suy ra điều kiện của \(k\).
Lời giải chi tiết:
Với \(m = 0\) ta có:\(y = {x^3}-4{x^2}-4x\).
Xét phương trình hoành độ giao điểm: \({x^3}-4{x^2}-4x = kx\) (2)
Đường thẳng \(y = kx\) cắt (C) tại ba điểm phân biệt nếu phương trình (2) có ba nghiệm phân biệt.
Có
\(\begin{array}{l}
\left( 2 \right) \Leftrightarrow {x^3} - 4{x^2} - 4x - kx = 0\\
\Leftrightarrow {x^3} - 4{x^2} - \left( {k + 4} \right)x = 0
\end{array}\) \( \Leftrightarrow x\left[ {{x^2} - 4x - \left( {k + 4} \right)} \right] = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} - 4x - \left( {k + 4} \right) = 0\,\,\left( 3 \right)\end{array} \right.\)
\(\left( 2 \right)\) có ba nghiệm phân biệt \( \Leftrightarrow \left( 3 \right)\) có hai nghiệm phân biệt khác \(0\)
\( \Leftrightarrow \left\{ \begin{array}{l}
\Delta ' = 4 + k + 4 > 0\\
{0^2} - 4.0 - \left( {k + 4} \right) \ne 0
\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l} k + 8 > 0\\-k -4\ne 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}k > - 8\\k \ne - 4\end{array} \right.\).
Vậy với \(k > - 8\) và \(k \ne - 4\) thì \(\left( C \right)\) cắt đường thẳng \(y = kx\) tại ba điểm phân biệt.

