Đề bài
Cho hình chóp \(S.ABCD\) có đáy là hình vuông, \(SA\) vuông góc với đáy, \(SA = AC\). Mặt phẳng qua \(A\) vuông góc với \(SC\) cắt \(SB,SC,SD\) lần lượt tại \(B',C',D'\). Tỉ số giữa thể tích hình chóp \(S.AB'C'D'\) và thể tích hình chóp \(S.ABCD\) là:
A. \(\dfrac{1}{6}\) B. \(\dfrac{1}{4}\)
C. \(\dfrac{1}{3}\) D. \(\dfrac{1}{2}\)
Phương pháp giải - Xem chi tiết
- Dựng mặt phẳng \(\left( {AB'C'D'} \right)\) và tính tỉ số các đoạn thẳng \(\dfrac{{SB'}}{{SB}},\dfrac{{SC'}}{{SC}},\dfrac{{SD'}}{{SD}}\).
- Tính tỉ số thể tích hai hình chóp bằng cách chia thành các hình chóp tam giác.
Lời giải chi tiết
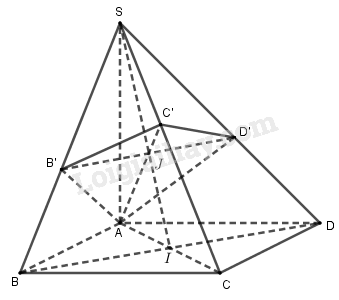
Ta có: \(\Delta SAC\) vuông cân và \(SC \bot AC'\) nên \(C'\) là trung điểm của \(SC\).
Gọi \(I = AC \cap BD\) và \(J = SI \cap AC'\).
Khi đó \(J\) là trọng tâm của \(\Delta SAC\).
Dễ thấy \(BD \bot \left( {SAC} \right) \Rightarrow BD \bot SC\).
Mà \(SC \bot \left( {AB'C'D'} \right)\) \( \Rightarrow BD// (AB'C'D')\).
Do đó \(BD//B'D'\) \( \Rightarrow \dfrac{{SB'}}{{SB}} = \dfrac{{SD'}}{{SD}} = \dfrac{{SJ}}{{SI}} = \dfrac{2}{3}\).
\( \Rightarrow \dfrac{{{V_{S.AB'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\) \( = 1.\dfrac{2}{3}.\dfrac{1}{2} = \dfrac{1}{3}\)
\(\dfrac{{{V_{S.AD'C'}}}}{{{V_{S.ADC}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SD'}}{{SD}}.\dfrac{{SC'}}{{SC}}\)\( = 1.\dfrac{2}{3}.\dfrac{1}{2} = \dfrac{1}{3}\)
\( \Rightarrow \dfrac{1}{3} = \dfrac{{{V_{S.AB'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{{V_{S.AD'C'}}}}{{{V_{S.ADC}}}}\) \( = \dfrac{{{V_{S.AB'C'}} + {V_{S.AD'C'}}}}{{{V_{S.ABC}} + {V_{S.ADC}}}} = \dfrac{{{V_{S.AB'C'D'}}}}{{{V_{S.ABCD}}}}\)
Vậy \(\dfrac{{{V_{S.AB'C'D'}}}}{{{V_{S.ABCD}}}} = \dfrac{1}{3}\).
Chọn C.

