Cho hàm số: \(y = {x^3}-3{x^2}\)
LG a
Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.
Phương pháp giải:
- Tìm TXĐ.
- Xét sự biến thiên.
- Vẽ đồ thị hàm số.
Giải chi tiết:
TXĐ: \(D = \mathbb{R}\).
Sự biến thiên: \(y' = 3{x^2} - 6x = 3x(x - 2)\); \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)
Hàm số đồng biến trên mỗi khoảng \(( - \infty ;0),(2; + \infty )\)
Hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\).
Hàm số đạt cực đại tại \(x = 0;{y_{CD}} = y\left( 0 \right) = 0\).
Hàm số đạt cực tiểu tại \(x = 2;{y_{CT}} = y\left( 2 \right) = - 4\).
Giới hạn: \(\mathop {\lim }\limits_{x \to \pm \infty } y = \pm \infty \)
Điểm uốn: \(y'' = 6x - 6,y'' = 0 \Leftrightarrow x = 1;\)\(y(1) = - 2\) suy ra đồ thị có điểm uốn \(I\left( {1; - 2} \right)\).
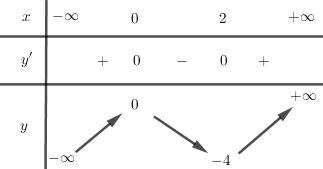
Bảng biến thiên:
Đồ thị:
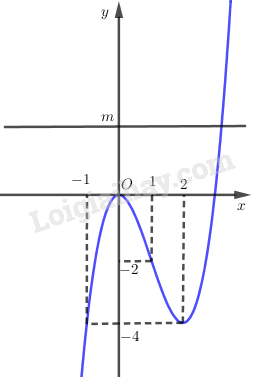
LG b
Tìm các giá trị của tham số \(m\) để phương trình \({x^3}-3{x^2}-m = 0\;\) có ba nghiệm phân biệt.
(Đề thi tốt nghiệp THPT năm 2008)
Phương pháp giải:
- Biến dổi phương trình về \({x^3} - 3{x^2} = m\).
- Biện luận số nghiệm của phương trình dựa vào số giao điểm của đồ thị hàm số vừa vẽ với đường thẳng \(y = m\) và kết luận.
Giải chi tiết:
Ta có: \({x^3} - 3{x^2} - m = 0\)\( \Leftrightarrow {x^3} - 3{x^2} = m\) (*)
Phương trình (*) có \(3\) nghiệm phân biệt khi và chỉ khi đường thẳng \(y = m\) cắt \(\left( C \right)\) tại \(3\) điểm phân biệt. Từ đó suy ra \( - 4 < m < 0.\)

