Giải bài 1.55 trang 23 SBT hình học 12

141 lượt xem

Đề bài

Cho hình hộp $ABCD.A'B'C'D'$ có đáy là hình chữ nhật, hình chiếu của $A'$ lên đáy $\left( {ABCD} \right)$ trùng với trung điểm của cạnh $AD$ . Biết rằng $AB = a,AD = 2a$ và thể tích hình hộp đã cho bằng $2{a^3}$ . Khoảng cách từ $B$ đến mặt phẳng $\left( {A'DCB'} \right)$ bằng:

A. $\dfrac{{\sqrt 2 }}{6}a$ B. $\dfrac{{\sqrt 2 }}{3}a$

C. $\dfrac{{\sqrt 3 }}{3}a$ D. $a\sqrt 2$

Phương pháp giải - Xem chi tiết

- Gọi $H$ là trung điểm của $AD$ , $E$ là hình chiếu của $H$ trên $A'D$ .

- Nhận xét: $d\left( {B,\left( {A'B'CD} \right)} \right) = d\left( {A,\left( {A'B'CD} \right)} \right)$ $= 2d\left( {H,\left( {A'B'C'D'} \right)} \right)$ và tính toán.

Lời giải chi tiết

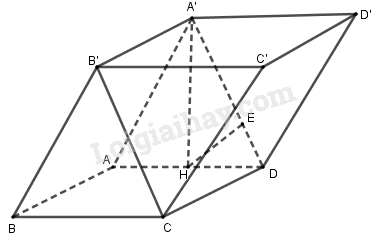
Gọi $H$ là hình chiếu của $A'$ trên $AD$ , $H$ là trung điểm của $AD$ , $E$ là hình chiếu của $H$ trên $A'D$ .

Ta có: ${S_{ABCD}} = AB.AD = 2{a^2}$ $\Rightarrow A'H = \dfrac{{{V_{ABCD.A'B'C'D'}}}}{{{S_{ABCD}}}} = \dfrac{{2{a^3}}}{{2{a^2}}} = a$ .

Dễ thấy $AB//\left( {A'B'CD} \right)$ $\Rightarrow d\left( {B,\left( {A'B'CD} \right)} \right) = d\left( {A,\left( {A'B'CD} \right)} \right)$ $= 2d\left( {H,\left( {A'B'CD} \right)} \right)$ .

Lại có $CD \bot \left( {ADD'A'} \right) \Rightarrow CD \bot HE$ . Mà $HE \bot A'D$ nên $HE \bot \left( {A'DCB'} \right)$ .

Do đó $d\left( {H,\left( {A'B'CD} \right)} \right) = HE$ .

Mà $HD = \dfrac{1}{2}AD = a,HA' = a$ nên $\dfrac{1}{{H{E^2}}} = \dfrac{1}{{H{D^2}}} + \dfrac{1}{{A'{H^2}}}$

$\Rightarrow HE = \dfrac{{HA'.HD}}{{\sqrt {A'{H^2} + H{D^2}} }}$ $= \dfrac{{a.a}}{{\sqrt {{a^2} + {a^2}} }} = \dfrac{{a\sqrt 2 }}{2}$ .

Vậy $d\left( {B,\left( {A'B'CD} \right)} \right) = 2HE = a\sqrt 2$ .

Chọn D.

SBT Toán lớp 12