Đề bài
Cho hình chóp tứ giác \(S.ABCD\) có thể tích bằng \(V\). Lấy điểm \(A'\) trên cạnh \(SA\) sao cho \(SA' = \dfrac{1}{3}SA\). Mặt phẳng qua \(A'\) và song song với đáy của hình chóp cắt các cạnh \(SB,SC,SD\) lần lượt tại \(B',C',D'\). Thể tích hình chóp \(S.A'B'C'D'\) bằng:
A. \(\dfrac{V}{3}\) B. \(\dfrac{V}{9}\)
C. \(\dfrac{V}{{27}}\) D. \(\dfrac{V}{{81}}\)
Phương pháp giải - Xem chi tiết
Chia khối chóp tứ giác thành hai khối chóp tam giác và tính tỉ số thể tích.
Sử dụng công thức tính tỉ số thể tích của hai khối chóp tam giác.
Xem tại đây.
Lời giải chi tiết
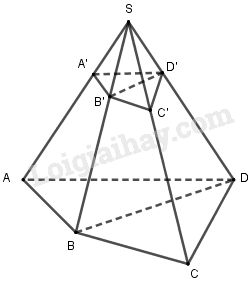
Dễ thấy \(B',C',D'\) thuộc các cạnh \(SB,SC,SD\) sao cho \(\dfrac{{SB'}}{{SB}} = \dfrac{{SC'}}{{SC}} = \dfrac{{SD'}}{{SD}} = \dfrac{1}{3}\)
Do đó \(\dfrac{{{V_{S.A'B'D'}}}}{{{V_{S.ABD}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SD'}}{{SD}}\) \( = \dfrac{1}{3}.\dfrac{1}{3}.\dfrac{1}{3} = \dfrac{1}{{27}}\);
\(\dfrac{{{V_{S.C'B'D'}}}}{{{V_{S.CBD}}}} = \dfrac{{SC'}}{{SC}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SD'}}{{SD}}\) \( = \dfrac{1}{3}.\dfrac{1}{3}.\dfrac{1}{3} = \dfrac{1}{{27}}\)
\( \Rightarrow \dfrac{1}{{27}} = \dfrac{{{V_{S.A'B'D'}}}}{{{V_{S.ABD}}}} = \dfrac{{{V_{S.C'B'D'}}}}{{{V_{S.CBD}}}}\) \( = \dfrac{{{V_{S.A'B'D'}} + {V_{S.C'B'D'}}}}{{{V_{S.ABD}} + {V_{S.CBD}}}} = \dfrac{{{V_{S.A'B'C'D'}}}}{{{V_{S.ABCD}}}}\)
\( \Rightarrow {V_{S.A'B'C'D'}} = \dfrac{1}{{27}}V\).
Chọn C.
