Đề bài
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a,BC = b,AA' = c\). Gọi \(E\) và \(F\) lần lượt là những điểm thuộc cạnh \(BB'\) và \(DD'\) sao cho \(BE = \dfrac{1}{2}EB',DF = \dfrac{1}{2}FD'\). Mặt phẳng \(\left( {AEF} \right)\) chia khối hộp chữ nhật \(ABCD.A'B'C'D'\) thành hai khối đa diện \(\left( H \right)\) và \(\left( {H'} \right)\). Gọi \(\left( {H'} \right)\) là khối đa diện chứa đỉnh \(A'\). Hãy tính thể tích của \(\left( H \right)\) và tỉ số thể tích của \(\left( H \right)\) và \(\left( {H'} \right)\).
Phương pháp giải - Xem chi tiết
- Tính thể tích các khối đa diện, sử dụng phương pháp phân chia khối đa diện.
- Từ đó suy ra tỉ số.
Lời giải chi tiết
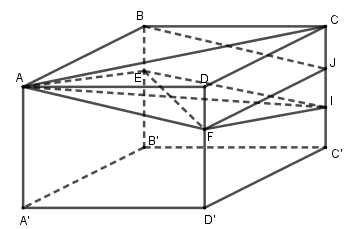
Gọi \(I = CC' \cap \left( {AEF} \right)\).
Vì \(\left\{ \begin{array}{l}\left( {AEF} \right) \cap \left( {ABB'A'} \right) = AE\\\left( {AEF} \right) \cap \left( {CDD'C'} \right) = FI\\\left( {ABB'A'} \right)//\left( {CDD'C'} \right)\end{array} \right.\) nên \(AE//FI\).
Tương tự \(AF//EI\) nên tứ giác \(AEIF\) là hình bình hành.
Trên cạnh \(CC'\) lấy điểm \(J\) sao cho \(CJ = DF\).
Dễ thấy \(FJ//CD//AB,\) \(FI = CD = AB\) nên \(ABJF\) là hình bình hành \( \Rightarrow AF//BJ,AF = BJ\).
Suy ra \(EI//BJ,EI = BJ\) hay \(EBJI\) là hình bình hành \( \Rightarrow BE = JI\).
Từ đó suy ra \(IJ = EB = DF = JC = \dfrac{c}{3}\)
Ta có \({S_{BCIE}} = \dfrac{1}{2}\left( {\dfrac{{c + 2c}}{3}} \right)b = \dfrac{{bc}}{2}\); \({S_{DCIF}} = \dfrac{1}{2}\left( {\dfrac{{c + 2c}}{3}} \right)a = \dfrac{{ac}}{2}\)
Nên \({V_{(H)}} = {V_{A.BCIE}} + {V_{A.DCIF}}\)\( = \dfrac{1}{3}.\dfrac{{bc}}{2}.a + \dfrac{1}{3}.\dfrac{{ac}}{2}.b = \dfrac{{abc}}{3}\)
Lại có \({V_{ABCD.A'B'C'D'}} = abc\) \( \Rightarrow {V_{(H')}} = \dfrac{2}{3}abc\)
\( \Rightarrow \dfrac{{{V_{(H)}}}}{{{V_{(H')}}}} = \dfrac{1}{2}\).

